
| Olympiades académiques de mathématiques 2002 Solutions |
| Antenne communication Bordeaux, le 27 mars 2002 |
Exercice 1
Soit :
v la vitesse de la colonie de fourmis en cm.s-1,
V la vitesse de la fourmi,
t1 le temps aller de la fourmi en secondes
et t2 le temps retour.

Exercice 2
a) Les trois formes sont : le carré, le triangle équilatéral et l’hexagone.
La démonstration, qui n’était pas demandée, part du principe que si on accole p formes identiques en un sommet A , l’angle de la forme en ce sommet étant a, on a p ´ a = 2p et d’autre part, puisque c’est un polygone régulier, si n est le nombre de côtés,
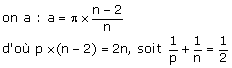
avec p et n entiers naturels supérieurs à 2.
Seuls les couples (3 ; 6), (4 ; 4) et (6 ; 3) conviennent d’où le résultat.
b) Parmi ces figures qui réalisent un pavage du plan par des polygones réguliers, c'est l’hexagone régulier qui a le plus petit périmètre, en effet :


Exercice 3
1. Quelle que soit la répartition obtenue, la somme des gains est égale à 3 ´ (1+2+….+10) = 165 puisque chaque numéro de 1 à 10 est compté 3 fois.
La moyenne des dix gains est donc égale à 16,5.
2. Il en résulte qu’il y a au moins un gain supérieur ou égal à 17 ; en effet, si tous les gains étaient inférieurs ou égaux à 16, leur somme serait inférieure ou égale à 10 ´ 16 donc à 160.
3. On peut construire une répartition pour laquelle tous les gains sont inférieurs ou égaux à 18 : on met à part le 1 et on répartit les 9 autres jetons par groupes de trois successifs ; chaque groupe de trois doit avoir une somme égale à 18 (puisque 55 = 1 + s1 + s2 + s3 et 1 + 3 ´ 18 = 55, où s1,s2 et s3 sont les trois sommes).
On examine alors les partitions de 18 en trois entiers distincts inférieurs ou égaux à 10 :
10 + 6 + 2 ; 10 + 5 + 3 ;
9 + 7 + 2 ; 9 + 6 + 3 ;
9 + 5 + 4 ; 8 + 7 + 3 ;
8 + 6 + 4 ; 7 + 6 + 5.
Le choix de 10 + 6 + 2 impose pour les deux
autre sommes 9 + 5 + 4 et 8 + 7 + 3
Le choix de 10 + 5 + 3 impose pour les deux autres sommes
9 + 7 + 2 et 8 + 6 + 4.
Dans chaque cas on peut fabriquer plusieurs solutions.
Exemple : 1, 10, 6, 2, 9, 5, 4, 8, 3, 7.
Dans ce cas les gains sont :17, 18, 17, 16, 18, 17, 15, 18, 11, 18.
4. Supposons tous les gains inférieurs ou égaux à 17.
En isolant le 1 et en répartissant 3 par 3 les autres jetons, la somme de tous
les jetons serait au maximum égale à 1 + 3 * 17 = 52
ce qui est impossible car 1 + 2 + … + 10 = 55.
Il y a donc au moins un gain supérieur ou égal à 18.
Exercice 4
1. Pour cette question il y a un grand nombre de réponses possibles qui ne posent aucun problème.
2. On peut partager le damier en deux rectangles 5 ´ 10 et remarquer que toute forme construite avec neuf carrés loge dans l’un de ces rectangles.
3. En observant la « longueur » et la « largeur » de chaque forme on constate que toute forme de neuf carrés loge dans un rectangle de taille 1 ´ 9 ; 2 ´ 8 ; 3 ´ 7 ; 4 ´ 6 ou 5 ´ 5, c’est à dire dans un rectangle de taille a ´ (10 - a) pour 0 < a £ 5. Or quatre copies identiques d’un tel rectangle peuvent être posées simultanément sur le damier sans chevauchement ; voir figure :
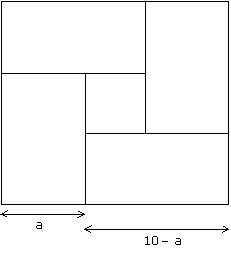
| En revanche, il n’est pas
possible de poser 5 croix. |
|