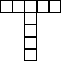
1) Dessiner l’une des solutions si on pose quatre exemplaires de la pièce représentée ci contre :
| Olympiades académiques de mathématiques 2002 Sujet |
| Antenne communication Bordeaux, le 27 mars 2002 |
27/03/2002
Classe de première
Durée : 4 heures.
Les quatre exercices sont indépendants. Les calculatrices sont autorisées.
Exercice 1
Des fourmis se déplacent, en ligne droite, à la queu leu leu, à
vitesse constante, en formant une colonne de 50 cm de long.
La dernière fourmi du groupe décide d’aller ravitailler la fourmi chef et pour
cela rejoint la tête de la colonne puis, sa mission étant accomplie, retourne
aussitôt à la queue de la colonne.
Sachant que, pendant cet aller retour, la vitesse de cette fourmi est restée constante et que la colonne a parcouru 50 cm, quelle est la distance parcourue par la fourmi ravitailleuse ?
Exercice 2
Les abeilles ont à déposer leur miel dans des alvéoles disposées
sur une surface plane donnée.
Elles vont paver cette surface au moyen de polygones réguliers juxtaposés, tous
identiques.
a) Quelles sont les trois formes qu’elles peuvent choisir pour réaliser ce pavage ? (on ne justifiera pas la réponse).
b) La construction de ces alvéoles doit être la plus économique
possible.
À aire égale, quel est, parmi les trois polygones réguliers possibles, celui
qui a le plus petit périmètre ?
Exercice 3
10 personnes sont assises autour d’une table ronde.
10 jetons portant les numéros de 1 à 10 sont distribués au hasard à ces dix
personnes.
Chaque personne gagne une somme égale, en euros, au total du numéro de son propre
jeton, de celui de son voisin de gauche et de celui de son voisin de droite.
1) À l’aide d’un procédé aléatoire de votre choix, donner un exemple
de répartition des jetons.
Sur cet exemple, indiquer le gain de chaque personne et la moyenne de ces dix
gains.
2) Prouver que, quelle que soit la répartition des jetons, au moins une des dix personnes aura un gain supérieur ou égal à 17 euros.
3) Donner un exemple où tous le gains sont inférieurs ou égaux à 18.
4) Peut-on, dans la deuxième question, remplacer 17 par 18 ?
Exercice 4
On dispose :
Le problème consiste à poser plusieurs exemplaires identiques de cette pièce sur le damier en respectant les règles suivantes :
|
 |
2) Montrer que, quelle que soit la forme de la pièce de départ, il est possible de poser deux exemplaires de cette pièce en respectant les règles ci dessus.
3) Peut-on dans la question précédente remplacer deux par trois, par quatre, par cinq, etc. ?