| Olympiades académiques de mathématiques 2003 Solutions |
| Antenne communication Bordeaux, le 22 mai 2003 |
Exercice 1
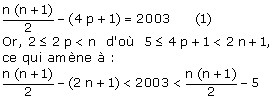
Soit n le nombre de pages du livre. Les pages collées sont une page de gauche de numéro pair 2p et une page de droite de numéro 2p + 1.Donc la somme de tous les nombres de 1 à n, hormis 2p et 2p + 1, est égale à 2003, soit :

Cette double inégalité conduit aux deux inéquations :
n² - 3n – 4008 < 0 (2)
Et n² + n – 4016 ³ 0 (3)
(2) donne n < 64,8 et (3) donne n > 62,9.
n étant entier on a n = 63 ou n = 64.
Si n = 63, on trouve p = 3 et si n = 64, on trouve p = 19.
Conclusion : ou bien le livre a 63 pages et les pages 6 et 7 sont collées, ou bien le livre a 64 pages et les pages 38 et 39 sont collées.
Exercice 2
1. Etude du cas « 1 ;5 »
Supposons que AB = x. On a donc AC = AD = BC = BD = CD = y.
Les triangles ACD et BCD sont équilatéraux. On a une seule configuration puisque A ¹ B.
2. Le cas « 2 ;4 »
a) Posons AB = CD = x.
On a donc AC = AD = BC = BD = y.
Le quadrilatère cherché est un losange dont les diagonales ont même longueur,
c’est un carré.
b) Posons AB = AC = x. On a donc AD = BC = BD = CD = y. Le triangle BCD est équilatéral. A est à l’intersection de la médiatrice de [BC] et du cercle de centre D et de rayon y. On a deux configurations.
3. Le cas « 3 ;3 ».
a) les trois segments de longueur x sont disposés en étoile. Par exemple, AB = AC = AD = x. On a donc, BC = BD = CD = y. le triangle BCD est équilatéral et A est le centre de ce triangle.
b) Si les trois segments de longueur x forment un triangle équilatéral, on retrouve la précédente configuration.
c) Il reste le cas où les trois segments de longueur x forment une chaîne ouverte. Posons AB = BC = CD = x. On a donc AC = AD = BD = y. les triangles BDA, ADC, ABC et BCD sont isocèles. Appelons O le point d’intersection des segments [BD] et [AC). Les triangles BDA et ADC d’une part, ABC et BCD d’autre part, sont isométriques. Les angles CAD et BDA d’une part, DBC et ACB d’autre part sont égaux. Puisque les angles BOC et AOB sont opposés par le sommet, ils sont égaux ce qui entraîne l’égalité des quatre angles précédents et le parallélisme des droites (BC) et (AD).
La configuration cherchée est donc un trapèze isocèle.
Exercice 3
|
|
Pour le premier carré AMNP, plusieurs méthodes sont rapides : Thalès ou la bissectrice ; dans tous les cas on obtient comme longueur du côté AM :
Pour le deuxième carré M’N’P’Q’ on peut utiliser l’homothétie de centre A qui transforme le carré BC’B’C. en le carré M’N’P’Q’. On obtient alors comme longueur du côté M’N’ : On peut alors comparer les aires des deux carrés ; on calcule x² - y² et, après calculs, on trouve : ceci étant toujours positif, c’est le premier carré qui a la plus grande aire. |
Exercice 4
On choisit comme repère orthonormal le repère de centre O le centre de la table et d’unité la longueur du carreau du quadrillage(0,5 m).
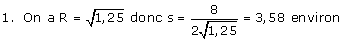
2. Les deux plus petites tables ont pour diamètres respectifs en
mètres 1 et 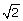 .
.
— Si d = 1, la table a quatre pieds d’où s = 4.
— 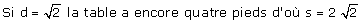
3. La table a 12 pieds la plus solide est la plus petite car, si N est constant,

Conclusion : la table à 12 pieds la plus solide est celle de diamètre 5 mètres. En conséquence, le coefficient de solidité maximum d’une table à 12 pieds est 2,4.
4. On peut montrer que toutes les tables sauf la plus petite ont un coefficient de solidité strictement inférieur à 4.
Conclusion : la table la plus solide est donc la plus petite…
5. Quand le rayon ou le diamètre de la table est un nombre entier
cela veut dire qu’il y a 4 pieds sur les axes. Donc, si une table à 16 pieds
a un diamètre en nombre entier, on doit avoir 3 pieds par quart de table sur
des intersections de joints. Pour des raisons de symétrie il doit y avoir un
pied sur la première bissectrice. Dans ce cas, on a R² = 2 a², où a est un
nombre entier ou décimal, et donc 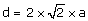 , avec 2a entier. Ceci
contredit le fait que le diamètre est un entier.
, avec 2a entier. Ceci
contredit le fait que le diamètre est un entier.
Conclusion : René ne pourra pas construire une table à 16 pieds dont le diamètre est un entier.