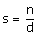26/03/2003
Classe de première
Durée : 4 heures.
Les quatre exercices sont indépendants. Les calculatrices sont autorisées.

Exercice 1

Les pages d’un livre sont numérotées de 1 à n (on rappelle que la page numérotée 1 est toujours une page de droite). On additionne les numéros de toutes les pages et on trouve un total égal à 2003. Mais deux pages numérotées sont restées collées et leurs numéros n’ont pas été comptés.

Quels sont le nombre de pages du livre et les numéros des pages collées ?

Exercice 2

On se propose de déterminer toutes les configurations de quatre points distincts A, B, C et D du plan tels que leurs distances mutuelles AB, AC, AD, BC, BD, CD ne prennent que deux valeurs exactement que l’on notera x et y. C’est par exemple le cas lorsque ABCD est un carré, x est la longueur des côtés et y celle des diagonales.

1. Etude du cas « 1 ; 5 » où l’une des distances est égale à x et les cinq autres à y.

Montrer qu’il existe, à l’ordre près des points, une seule configuration répondant à la question.

Dessiner cette configuration.

2. Etude du cas « 2 ; 4 » où deux distances sont égales à x et les quatre autres à y.

a. On suppose que les deux segments de longueur x n’ont pas de sommet commun.

Quelle configuration obtient-on ? La dessiner.

b. Que se passe-t-il lorsque les deux segments de longueur x ont un sommet en commun ?

3. Etudier le cas « 3 ; 3 ».

Exercice 3

Etant donné un triangle ABC rectangle en A, on note : AB = c, AC = b et BC = a.

On veut construire deux carrés inscrits dans ce triangle : le premier ayant A pour sommet, le second ayant un côté porté par l'hypoténuse.

1. Expliquer pour chacun d'eux comment réaliser la construction.

2. Exprimer les côtés x et y de ces deux carrés en fonction de b et c puis comparer leur aire.

Exercice 4

René dispose dans son jardin d’une très grande terrasse carrelée avec de très belles dalles carrées de 0,5 m de côté. Il décide de construire sur cette terrasse une table ronde avec les pieds sur le bord et un parasol central.

René est un bricoleur prévoyant, aussi, pour gagner en stabilité, il décide que la table devra avoir le maximum de pieds, tous solidement fixés dans le sol. Tout comme le parasol car on n’est jamais à l’abri d’un coup de vent…

Mais René est aussi un bricoleur soigneux ; alors pour ne pas détériorer les dalles, il choisit de percer la terrasse uniquement aux intersections des joints de séparation.

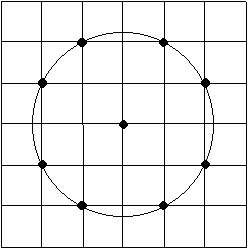
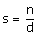
La figure ci-contre donne un exemple de table à 8 pieds. Si n désigne le nombre de pieds de la table et d son diamètre exprimé en mètres, on définit le coefficient de solidité s de la table par la formule : Une table est donc d’autant plus solide que son coefficient de solidité est élevé.

1. Calculer le coefficient de solidité de la table dessinée ci dessus.

2. Quelles sont les deux tables les plus petites ? Préciser leur coefficient de solidité.

3. Quel est le coefficient de solidité maximal d’une table à 12 pieds ?

4. Quelle est la table la plus solide ?

5. René peut-il fabriquer une table à 16 pieds dont le diamètre exprimé en mètres est un nombre entier ?