Liaison Troisième / Seconde Mérignac/Pessac : atelier de mathématiques

Atelier de mathématiques

	Zone d'Animation Pédagogique de Mérignac-Pessac Réunion du 29 janvier 2003 (après midi) au lycée Fernand Daguin de Mérignac (Gironde)

L'atelier de mathématiques de cette réunion s'est axé sur le calcul littéral ou algébrique, de la classe de sixième à celle de seconde.

Le calcul littéral ou algébrique pose en effet de nombreux problèmes aux élèves, tant au collège qu'au lycée, alors que l'on note une plus grande aisance de leur part dans les travaux géométriques. C'est un facteur d'échec important en Mathématiques et de difficultés sérieuses en Sciences physiques ; c'est pourquoi ce thème a été choisi pour le travail en atelier disciplinaire.

Les collègues présents se sont répartis dans deux groupes qui ont adopté des démarches voisines et étudié les points suivants :

I - Programmes : difficultés liées au calcul littéral ou algébrique

II - Travail en groupes sur le calcul littéral de la sixième à la seconde, puis synthèse.

I - Programmes : difficultés liées au calcul littéral ou algébrique

— Examen des programmes et de leurs objectifs de la sixième à la seconde, en ce qui concerne le calcul littéral au collège et le calcul algébrique au lycée : mise en évidence de la continuité des programmes.

— Nécessité d'une introduction prudente et très progressive des notions de calcul littéral au collège ; historiquement, cette notion a été très longue à installer ; ce n’est qu’au XVI^e siècle que l’on atteint, avec François Viète, le stade de l'algèbre symbolique : désormais les lettres sont utilisées non seulement pour représenter des quantités inconnues mais également pour désigner des données ; il devient alors possible d'exprimer des solutions générales de problèmes et d'utiliser l'algèbre comme outil pour prouver des règles de calcul.

— Difficultés rencontrées par les élèves : examen des exercices d’une page d’un cahier d'évaluation de début de seconde (l’évaluation en début de seconde ne se fait plus, mais il demeure possible, et même conseillé, d’utiliser les anciens cahiers pour concevoir des évaluations à distribuer au fil de l’année et du déroulement du travail). Mise en évidence de la difficulté du passage de «l'arithmétique » pratiquée à l’école primaire au calcul littéral en collège ; erreurs provenant d’une mauvaise compréhension des différents statuts de la lettre et de l’égalité, ce dernier étant perçu par certains collègues comme encore plus délicat à faire passer aux élèves que celui de la lettre (distinction entre le signe "=" de la table de multiplication, le signe "=" de définition d'une expression f(x) = 2x + 4, le signe "=" de l'équation et enfin celui de l'identité que l'élève doit mémoriser k(a + b) = ka + kb) ; erreurs dues peut-être également à un apprentissage trop rapide, à une suppression trop hâtive du signe "multiplié " dans certaines écritures (du type 6 (x + 5) par exemple) etc. (on pourra consulter à ce sujet le dossier "Calcul littéral au collège") ; idées de séquences de remédiation.

Partage des difficultés d'utilisation des puissances de 10 en Physique ; elles ont été vues en mathématiques en quatrième, de façon ponctuelle et peu ou pas réinvesties par la suite.

— Invitation à bien connaître les étapes du programme du collège, pour les collègues enseignant en lycée, et ce qui est attendu en seconde pour les collègues enseignant en collège.

II - Travail en groupes sur le calcul littéral de la sixième à la seconde, puis synthèse.

1. Une situation est proposée aux collègues

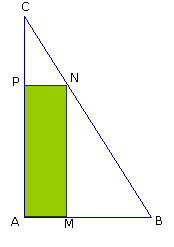
On considère un triangle ABC rectangle en A.

On donne AB = 6 et AC = 12.

AMNP est un rectangle. AM est variable.

Il s’agit d’essayer d’élaborer des énoncés d’exercices adaptés à chaque niveau (6^e, 5^e, 4^e, 3^e, 2^e) à partir de ces données, plus ou moins complétées, pour construire des situations utilisant le calcul algébrique dans ces différents niveaux, autour de la notion d’aire ou de périmètre.

À travers ces exercices, on cherche à faire évoluer la notion de lettre, ainsi que son statut.

2. Travail en ateliers

3. Mise en commun des travaux

3.a. Les exercices proposés par les collègues sont présentés ci-après, de façon succincte et sans rappeler les données de départ.

En 6^e

Faire construire la figure

APNM est un rectangle MB = 1 et AP = 2.

Calculer AM

Calculer l’aire et le périmètre du rectangle

La longueur AM et l’aire du rectangle étant données, trouver AP.

On peut faire compléter un tableau : on donne différentes valeurs pour AM et on fait calculer les valeurs correspondantes de MB ; on fait sentir la notion de longueur variable.

En 5^e

On pose AM = x

Exprimer MB à l’aide de x (pour introduire "en fonction de")

Calculer MB lorsque x = 5, x = 3, x = 2/3.

Ce qui suit a été abordé dans un seul des deux groupes :

En 4^e

1) On donne AM = 2 ; calculer CP, AP et l’aire du rectangle APNM

2) On pose AM = x ; exprimer CP et AP à l’aide de x et vérifier pour x = 2 ; exprimer l’aire du rectangle APNM en fonction de x et vérifier pour x = 2

3) Déterminer x pour que APNM soit un carré. Calculer l’aire dans ce cas.

En 3^e

Même version qu’en quatrième, en ajoutant la question : quelles sont les valeurs possibles de x ?

Une autre version possible :

Exprimer AP en fonction de x. Déterminer le périmètre du rectangle et tester s’il peut prendre une valeur donnée. Exprimer l’aire du triangle MNB en fonction de x, et trouver pour quelle valeur de x l’aire vaut 4, en guidant les élèves vers une "équation produit".

Il peut être intéressant de présenter aux élèves des courbes qui ne soient pas des droites ; une partie de ce qui est proposé dans III- Prolongement (ci-dessous) peut être adapté en classe de 3e.

En 2^e

On pose AM = x

On considère la fonction A qui à tout x associe l’aire du rectangle APNM. Exprimer A(x).

On étudie la fonction A : ensemble de définition, étude des variations en guidant les élèves, tableau de valeurs et représentation graphique que l’on exploitera.

3.b. La mise en commun des exercices élaborés par chaque groupe permet de dégager les idées principales et surtout les différentes étapes dans l’utilisation de la lettre.

En 6^e	Employer seulement une formule avec substitution (donner aire ou périmètre et longueur, trouver la largeur) Compléter une "égalité à trou"
En 5^e	Introduire la notion de variable (exprimer "en fonction de") Calculer avec différentes valeurs de x. Tester si une égalité (ou une inégalité simple) est vraie Résoudre des équations simples en utilisant uniquement le sens des opérations
En 4^e	Développer, réduire une expression. Résoudre une équation du premier degré. La lettre peut prendre différents statuts : elle peut être une variable à laquelle on donne différentes valeurs, une inconnue,…
En 3^e	Utiliser les factorisations et les égalités remarquables. Encadrer x, poser le problème de la validité d’une solution. Résoudre une "équation produit"
En 2^e	Utiliser les connaissances du collège à travers des situations de problèmes. Étudier des fonctions en utilisant les fonctions de référence : variations, tableau de valeurs. Tracer des représentations graphiques. Exploiter ces représentations

III- Prolongement

L'exercice suivant n'a pas été examiné en réunion ; il est de ceux qui peuvent être proposés en fin de collège et en début de lycée ; en enlevant la dernière question, celui-ci peut être posé en troisième et il peut l'être également en seconde en changeant éventuellement certaines consignes et en les adaptant un peu. Le tableau de valeurs permet aux élèves de voir «bouger » l’aire quand x varie, et de mieux sentir la notion de fonction ; c’est une notion difficile, dont la mise en place débute en troisième et se poursuit tout au long du lycée.

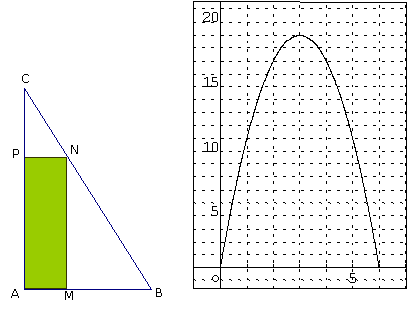
ABC est un triangle rectangle en A tel que AB = 6 cm et AC = 12 cm. Le point M décrit le segment [AB]. Le réel x désigne, en cm, la longueur AM. On construit le rectangle AMNP où N appartient à [BC] et P appartient à [AC]. On appelle f(x) l’aire, en cm², du rectangle AMNP. On admet que (C) est la courbe représentative de f dans le repère (O, I, J) ou .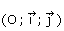

1. Faire une figure, placer le point M tel que AM = (2/3)AB, tracer le rectangle AMNP et calculer son aire. Retrouver ce résultat sur le graphique en laissant apparents les tracés utilisés.

2. Compléter le tableau suivant :

Longueur AM x	0	1	2	2,5	3	4	6
Aire du rectangle f(x)	0	10

3. Pour quelle position de M l’aire du rectangle AMNP semble-t-elle maximale ? Qu’avez-vous utilisé pour répondre : le graphique, la figure ou le tableau ?

4. Exprimer en fonction de x l’aire f(x) du rectangle AMNP.

5. Vérifier que f(x) = 18 – 2 (x - 3)². En déduire alors que f(x) £ 18.