Algorithme de Babylone

Équipe Acacadémique Mathématiques,
Bordeaux, 2002

 

Destination

Professeurs

Niveau

Terminale L, ooption facultative, nouveaux programmes

Type

Papier et TICE (tableur). Fichiers babylone.123, babylone.xls

Commentaires

Sur la base d’un texte historique on introduit une méthode de calcul de la racine carrée d’un nombre A à l’aide de suites récurrentes. Cette activité peut être utilisée clé en main à l’aide des fichiers tableurs joints ou il peut être demandé aux élèves de construire les suites afin d’étudier leur convergence.

 

Problème

img 1

img 2

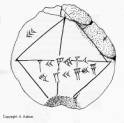
Il existe un très ancien document babylonien donnant une approximation de la racine de 2 sous la forme 1 24 51 10 en sexagésimal, c’est-à-dire, en décimal : 1,414 212 963, au lieu de 1,414 213 562.
Cliquer ici pour trouver une image, avec des commentaires, sur un site en anglais

Les historiens des mathématiques se sont interrogés pour savoir comment les Babyloniens avaient obtenu cette excellente approximation. On trouvera une réponse possible dans une activité, sur ce site, ainsi qu'une autre activité basée sur un texte d’Euler.

 

Modélisation

Un rectangle R1 d'aire A a pour dimensions x1 et y1.
On fabrique le rectangle R2 de dimensions
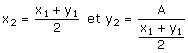
dimensions
donc de même aire que le rectangle R1.
En itérant le processus on va « se rapprocher » d’un carré d’aire A.
Créer à l’aide d’un tableur les suites des valeurs des nombres xn et yn ; comparer les résultats obtenus à 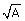racine(A) .