Nouveaux programmes en série S.T.G. |
Réunion nouveaux programmes de maths en série
STG |
Sommaire de cette page |
Ce document au format PDF (340 Ko) (préférable pour l'impression) |
Organisation et finalités de la série S.T.G.
Une présentation sous forme de diaporama
Intentions et objectifs des programmes
Intentions
L’épreuve de mathématiques au baccalauréat S.T.G.
Justification du choix de la méthode des moindres carrés pour un ajustement linéaire.
Résolution d’un problème d’optimisation
Statistiques et utilisation de sites de statistiques
Réalisation de diagrammes en boîtes
Exemples d’activités avec la calculatrice
Suites arithmétiques et géométriques
Utilisation de la calculatrice en tableur
Éclairage sur le vocabulaire économique ; exemples d’activités transdisciplinaires
Trois sessions de formation ont été organisées dans l’académie :
● Le 16 novembre 2005 au Lycée Élie Faure de Lormont (33)
● Le 23 novembre 2005 au Lycée Saint Cricq de Pau (64)
● Le 18 janvier 2006 au Lycée Victor Louis de Talence (33).
Programme de ces réunions :
| Matin |
Organisation et finalités de la série STG |
|
| Intentions et objectifs des programmes |
||
| L'épreuve de mathématiques au baccalauréat S.T.G. |
||
| Exemples d'activités T.I.C.E. à utiliser en classe |
||
| Après-midi |
Deux ateliers tournants |
|
| Exemples d'activités avec la calculatrice |
Éclairage sur le vocabulaire économique et exemples d'activités transdisciplinaires |
|
Organisation et finalités de la série
S.T.G. ![]()
La refonte de la série s’est faite dans l’optique d’une filière articulée à la fois sur l’enseignement secondaire (1re et Tale) et sur l’enseignement supérieur (B.T.S., D.E.C.F., …).
Cette rénovation se fait en lien avec le L.M.D. et l’évolution des emplois ; le secteur tertiaire offre des emplois essentiellement au niveau BAC+2.
Dans cette optique, le bac S.T.G. doit devenir un tremplin vers la poursuite d’études au minimum en B.T.S. ; ceci a induit une nouvelle architecture des programmes organisés autour de notions et de contenus.
Cette refonte, à l’initiative de l’Inspection d’Économie-Gestion, a pour but de redonner des lettres de noblesse à la série tertiaire.
Dans ce contexte, les nouveaux programmes de mathématiques ont pour objectif la préparation aux études supérieures courtes en assurant la continuité avec la classe de seconde.
Par ailleurs, l’orientation des élèves en fin de seconde vers la série S.T.G. devra prendre en compte les nouvelles exigences de cette série au niveau des compétences en mathématiques.
Les programmes de mathématiques ont été publiés au bulletin officiel :
Classe de première :
B.O. HS n° 5 - 9 septembre 2004
ftp://trf.education.gouv.fr/pub/edutel/bo/2004/hs5/maths_STG.pdf
Classe de terminale :
B.O. hors série n°7 du 1er septembre 2005
ftp://trf.education.gouv.fr/pub/edutel/bo/2005/hs7/mathematiques_stg.pdf
Document d’accompagnement : le projet est accessible à l’adresse
http://eduscol.education.fr/D0015/doc_acc_STG.pdf
Une présentation sous forme de diaporama ![]()
Ce diaporama est le fruit d’un travail effectué dans l’Académie de Versailles
Voir ou télécharger le diaporama (PDF : 70 Ko)
Intentions et objectifs des programmes ![]()
Intentions
Le programme de mathématiques en série S.T.G. doit apporter un éclairage sur les notions utilisées dans les disciplines technologiques ; les mathématiques permettant d’expliquer et de justifier l’utilisation des outils faite dans les autres matières.
Cela va induire un travail collaboratif étroit entre les enseignants de mathématiques et leurs collègues des disciplines technologiques.
« Du travail personnel en dehors du temps d’enseignement doit être proposé aux élèves sous différentes formes : »
● résolution d’exercices d’entraînement ;
● travaux individuels de rédaction réguliers et fréquents mais de longueur modeste.
Les devoirs de contrôle peuvent combiner :
● des exercices d’application du cours ;
● des questions de cours ;
● des problèmes plus synthétiques ou plus ouverts.
On pourra se référer au document de l’Inspection Générale de Mathématiques :
Les travaux écrits des élèves en mathématiques au collège et au lycée
« Les élèves doivent maîtriser l’emploi d’une calculatrice graphique dans les situations liées au programme de la classe. »
Le problème posé dans ces sections par l’achat d’une calculatrice performante en classe de première devrait être anticipé au sein de l’établissement, dès la classe de seconde car :
● d’une part, les exigences sur l’emploi d’une calculatrice deviennent quasi identiques dans toutes les séries ;
● d’autre part, les problèmes liés au financement seraient plus facilement couverts par le biais de l’allocation de rentrée versée en seconde et non en première.
Les enseignants résoudront plus facilement les problèmes liés à la multiplication des modèles de calculatrices au sein d’un classe avec l’aide de la brochure éditée par l’I.R.E.M. de Lyon : « 36 élèves, 36 calculatrices » qu’il est possible de commander (CD-ROM) à l’adresse suivante :
http://sierra.univ-lyon1.fr/irem/le3636.htm
On trouve sur ce document des exemples concrets et pratiques d’utilisation des différents modèles usuels de calculatrices (Casio, TI, HP et Sharp).
« L’emploi en mathématiques des outils informatiques est désormais indispensable :
● utilisation des micro-ordinateurs par les élèves ;
● utilisation en classe entière d’un micro-ordinateur équipé d’un système de vidéo-projection. »
L’évaluation des compétences au baccalauréat se fera sous forme d’exercices du type de ceux de la série de 1re littéraire (programme de mathématiques informatique).
La difficulté essentielle est due au fait qu’il n’existe aucun horaire dédoublé en mathématiques dans la série S.T.G. ; néanmoins l’utilisation des outils T.I.C.E. par les élèves est incontournable (en particulier l’usage du tableur).
Il convient donc d’essayer trouver des solutions pour remédier à l’absence de dédoublements en mathématiques.
Quelques pistes possibles :
● si les conditions matérielles locales le permettent (salle informatique suffisamment grande, disponibilité d’un assistant d’éducation, …), une demi-classe travaille sur les micro-ordinateurs pendant que l’autre moitié effectue un travail écrit (solution préconisée par l’Inspection Générale) ;
● achat par l’établissement d’un lot de calculatrices TI 83 Plus, d’un tablette de rétroprojection et du logiciel « Tableur » en version établissement édité par T.I. ; il s’agit d’un véritable tableur tournant sur calculatrice et permettant l’apprentissage des notions listées dans le programme de la série S.T.G.. Le problème du financement pouvant être résolu par l’apport de la « Taxe d’apprentissage » qu’est susceptible de toucher tout établissement ayant des séries technologiques ;
● travail étroit en collaboration avec les collègues des disciplines technologiques qui eux travaillent en demi-classe sur les micro-ordinateurs et peuvent donc faire manipuler les élèves sur des activités qui ont été préparées en cours de mathématiques. Cette approche est particulièrement intéressante car elle permet d’apporter l’éclairage et l’approche des mathématiques dans les disciplines tertiaires et de faire mieux sentir aux élèves le lien entre les mathématiques et les différents outils technologiques qu’ils utilisent régulièrement.
L’épreuve de mathématiques au baccalauréat
S.T.G. ![]()
La durée de l’épreuve de mathématiques ainsi que son coefficient ont été publiés au B.O. n° 31 du 1er septembre 2005.
http://www.education.gouv.fr/bo/2005/31/MENE0501605A.htm
| Coefficient |
Nature de l'épreuve |
Durée |
Total des coefficients |
| Spécialité "Communication et gestion des ressources humaines" |
|||
| 2 |
écrite |
2 heures |
40 ou 42 |
| Spécialité "Mercatique (marketing)" |
|||
| 3 |
écrite |
3 heures |
40 ou 42 |
| Spécialité "Comptabilité et finance d'entreprise" |
|||
| 3 |
écrite |
3 heures |
40 ou 42 |
| Spécialité "Gestion des systèmes d'information" |
|||
| 4 |
écrite |
3 heures |
40 ou 42 |
Une banque d’exercices (sur un modèle équivalent à ce qui a été proposé pour les séries E.S. et S.) sera mise en ligne prochainement.
Le formulaire est supprimé pour le baccalauréat 2007, cependant certaines formules peuvent être rappelées dans le sujet.
Il s’agit d’activités utilisables en classe entière à l’aide d’un micro-ordinateur relié à un vidéoprojecteur.
Justification du choix de la méthode
des moindres carrés
pour un ajustement linéaire ![]()
L’ajustement linéaire d’une série statistique quantitative à deux variables apparaît dans le programme de terminale pour toutes les spécialités.
| Contenus |
Capacités attendues |
Commentaires |
| Étude de séries de données statistiques quantitatives à deux variables. |
|
On accompagne ce travail d'un entretien des capacités sur les statistiques à une variable de la classe de première. |
| Nuage de points, point moyen. |
Associer un tableau de données à la suite (xk ; rk), 1 < k < N , où N est l'effectif de la population. |
|
|
|
Représenter graphiquement un nuage de points et déterminer le point moyen. |
Le point moyen a pour coordonnées
|
| Ajustement affine.
|
Trouver une fonction affine qui exprime de façon approchée y en fonction de x. Utiliser cette fonction pour interpoler ou extrapoler. |
L'objectif est d'étudier le lien éventuel entre deux caractères d'une même population. L'ajustement est réalisé soit par une méthode graphique, soit par la méthode des moindres carrés à l'aide de la calculatrice ou du tableur. |
| Séries chronologiques. |
Utiliser un ajustement affine pour faire une prévision. |
|
Le commentaire du programme est très clair sur les méthodes à utiliser :
● soit un ajustement graphique (celui-ci pouvant ensuite conduire à la recherche de l’équation de la droite d’ajustement) ;
● soit la méthode des moindres carrés à l’aide de la calculatrice ou du tableur (aucun calcul à la main ne peut donc être exigé des élèves).
Il a bien été précisé lors des journées inter-académiques de Toulouse que :
« l’utilisation de la méthode des moindres carrés est un exigible du programme de la série S.T.G. »
Le projet de document d’accompagnement (page 18) donne une idée d’activité intéressante :
« On peut néanmoins en expliquer le principe : pour
une droite donnée d'équation y = ax + b, on compare les
yi observés aux ![]() calculés (autrement dit les axi + b)
en calculant les résidus yi – axi + b). On souhaite trouver une
droite pour laquelle ces résidus soient les plus faibles possibles.
calculés (autrement dit les axi + b)
en calculant les résidus yi – axi + b). On souhaite trouver une
droite pour laquelle ces résidus soient les plus faibles possibles.
La droite des moindres carrés, ou droite de régression, est celle qui minimise la somme des carrés de ces résidus. »
Exemple (page 23) :
« Au cours d'une période d'hiver, le chargé de maintenance d’une entreprise a relevé certains jours la température X extérieure moyenne de la journée, et la consommation Y de fioul de la chaudière pendant la même journée. Il a obtenu le tableau suivant : »
| X (en degrés) |
-6 |
-5 |
-3 |
-2 |
-1 |
1 |
2 |
3 |
5 |
6 |
| Y (en litres) |
400 |
390 |
360 |
330 |
310 |
290 |
260 |
250 |
200 |
190 |
Une possibilité de travail à proposer aux élèves :
1. Construire le nuage de points.
2. Placer le point moyen G.
3. Tracer les différentes droites proposées sur la fiche annexe.
4. Compléter cette fiche afin de comparer la somme des carrés des résidus (il s’agira soit d’un travail papier, soit d’un travail sur micro-ordinateur).
5. Déterminer la droite d’ajustement par la méthode des moindres carrés.
6. Calculer pour cette droite la somme des carrés des résidus.
Remarques :
Les différentes droites proposées passent toutes par le point moyen du nuage ;
Le fichier tableur proposé (ajt_lin_elv2) permet le tracé automatique des différentes droites d’ajustement afin de ne faire travailler les élèves que sur l’utilisation des formules, des adressages relatifs et absolus et des recopies de cellules.
Les fichiers tableur proposés :
|
|
Excel |
OpenOffice StarOffice |
| Fiche de travail papier |
ajt_lin_elv1.xls |
ajt_lin_elv1.sxc |
| Fichier élève |
ajt_lin_elv2.xls |
ajt_lin_elv2.sxc |
| Fichier corrigé |
ajt_lin_cor.xls |
ajt_lin_cor.sxc |
| Téléchargement |
Fichier Compressé (15 Ko) |
Fichier Compressé (47 Ko) |
Résolution d’un problème d’optimisation ![]()
Les problèmes d’optimisation à deux variables et de régionnement du plan apparaissent dans les programmes de terminale de toutes les spécialités sauf CGRH.
| Contenus |
Capacités attendues |
Commentaires |
| Optimisation à deux variables Droite d'équation ax + by = c |
Représenter la droite d'équation ax + by = c |
Faire le lien avec la forme y = mx + p ou x = k |
| Régionnement du plan. |
Caractériser analytiquement un demi-plan. |
Exemples : coût constant, profit constant. Caractérisation d'un demi-plan par une inéquation du type ax + by > c ou ax + by £ c Exemple : seuil de rentabilité à deux produits. |
|
|
Résoudre graphiquement un système d'inéquations linéaires. Caractériser une région polygonale convexe donnée. |
Une région polygonale convexe étant représentée dans un repère du plan, on la caractérise par un système d'inéquations linéaires. |
| Programmation linéaire. |
Résoudre graphiquement un problème qui conduit à maximiser ou minimiser une expression du type ax + by sous plusieurs contraintes linéaires. |
Exemples : profit maximal. coût minimal. Dans le cas d'une recherche de solutions entières, on peut aborder quelques situations où la résolution peut être étudiée avec un tableur. |
Le projet de document d’accompagnement (page 4) donne des précisions et des idées d’activités intéressantes :
« Les équations de droite sont abordées sous la forme ax + by = c, utile dans les problèmes de programmation linéaire (droite de niveau c). Le lien avec les équations y = mx +p ou x = k rencontrées les années précédentes doit être souligné. Le programme vise une bonne maîtrise de la résolution graphique d’un système d’inéquations linéaires, mais aussi de la caractérisation d’une région polygonale convexe donnée par un système d’inéquations linéaires.
Dans le cas d’une recherche de solutions entières, le tableur permet soit le calcul effectif des valeurs d’une expression du type ax + by et la traduction des contraintes à l’aide l’instruction conditionnelle si… alors, soit la recherche de l’extremum à l’aide d’un solveur. Seule, l’utilisation d’un solveur sera reprise ultérieurement en économie gestion. En classe terminale, les trois approches « résolution graphique », « programmation d’une feuille de calcul » et « usage d’un solveur » se complètent. »
Exemple (page 15) :
« Une société de communication négocie des droits d’exploitation sur plusieurs années d’une chaîne de télévision à couverture nationale. Un contrat l’oblige à diffuser pendant cette période au moins 1800 heures de fictions françaises, 1800 heures de fictions européennes et 1200 heures de reportages.
Pour acheter les programmes, elle se fournit auprès de deux entreprises de production télévisuelle qui vendent des ensembles d’émissions « clé en main » appelés « lots ».
La société Damol propose des lots composés de la manière suivante :
● 90 heures de fictions françaises
● 120 heures de fictions européennes
● 40 heures de reportages
Chaque lot coûte 20 000 M€.
La société Martel propose des lots composés de la manière suivante :
● 90 heures de fictions françaises
● 60 heures de fictions européennes
● 100 heures de reportages
Chaque lot coûte 24 000 M€.
Déterminer l’achat qui permet de minimiser le coût des programmes achetés par la société de communication. »
Une possibilité de travail à proposer aux élèves :
1. Traduction de la situation :
On appelle x le nombre de lots achetés à la société Damol et y le nombre de lots achetés à la société Martel.
On aura les contraintes :

et il faut minimiser la quantité 20 x + 24 y.
2. Construction d’une feuille de calcul traduisant les contraintes et recherche expérimentale d’une solution en faisant varier les valeurs des cellules F2 et F3.
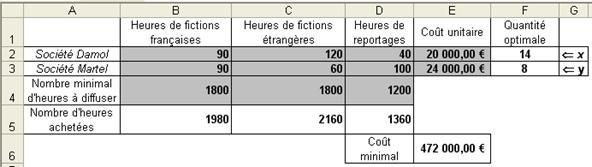
3. Étude des lignes de niveau de la fonction f définie par f (x ; y) = 20 x + 24 y en prenant en compte les différentes contraintes à l’aide de la fonction SI du tableur :
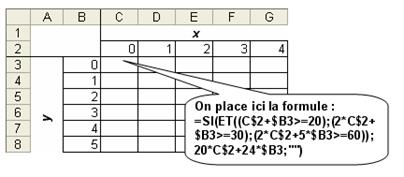
La ligne 2 contenant les valeurs de x, la colonne B celles de y ; il suffit ensuite de rechercher parmi les cellules contenant une valeur pour f ( x ; y ) (c'est-à-dire celles pour lesquelles x et y satisfont aux contraintes imposées) celle(s) qui a(ont) la valeur minimale.
Cette approche ayant l’avantage de bien faire saisir aux élèves ce que l’on cherche à minimiser.
4. Utilisation de l’outil Solveur du tableur (ceci nécessite d’utiliser le tableur Excel et d’avoir au préalable installé l’outil Solveur par : Outils è Macros Complémentaires ; choisir Complément Solver et cliquer sur Ok. Attention : le CD d’Office sera requis).
On reprend dans ce cas la feuille de calcul de la deuxième partie ; la recherche manuelle effectuée précédemment permettant d’éclairer ce que fait cet outil.
|
5. Résolution graphique par régionnement du plan : La correction pourra s’appuyer sur un fichier Géoplan. Les différentes commandes de la figure (listées ci-dessous) vont permettre de faire apparaître le régionnement du plan, puis la droite de coût : 20 x + 24 y
|
|
Les touches 1, 2, 3 et 4 permettent de faire apparaître les objets suivants :
Touche 1
la droite d'équation x + y = 20 ;
son équation ;
le demi-plan vérifiant x + y <20.
Touche 2
la droite d'équation 2 x + y = 30 ;
son équation ;
le demi-plan vérifiant 2 x + y < 30.
Touche 3
la droite d'équation 2 x + 5 y = 60 ;
son équation ;
le demi-plan vérifiant 2 x + 5 y < 60
Touche 4
la droite d'équation 20 x + 24 y = p et son équation, p étant un paramètre entier dont on peut modifier la valeur à l'aide des flèches du clavier;
un point M mobile à la souris sur cette droite et les coordonnées de ses projections sur les axes.
Lorsque l'on a minimisé la valeur de p en restant dans les contraintes les valeurs de x et y s'affichent.
Les fichiers tableur et Géoplan proposés :
|
|
Excel |
OpenOffice StarOffice |
| Fichier Géoplan |
prog_lin.g2w |
prog_lin.g2w |
| Fichier tableur élève |
prog_lin.xls |
prog_lin.sxc |
| Fichier tableur corrigé |
prog_lin_cor.xls |
prog_lin_cor.sxc |
| Téléchargement (Fichiers tableur et Géoplan) |
Fichier compressé (19 Ko) |
Fichier compressé (25 Ko) |
« On se contente en première STG d’introduire le nombre dérivé, dont la compréhension nécessite une longue maturation. La fonction dérivée sera traitée en classe terminale. »
Il a bien été précisé lors des journées inter-académiques de Toulouse que :
« La fonction dérivée n'est enseignée qu'en terminale, afin d'éviter des confusions par son introduction trop rapide ; il convient de travailler en classe de première autour du concept de nombre dérivé (vitesse, coût marginal, petits taux d'accroissements). »
| Contenus |
Capacités attendues |
Commentaires |
| Nombre dérivé et tangente |
|
|
| Approche graphique du concept de nombre dérivé d'une fonction en un nombre réel. |
Lire graphiquement un nombre dérivé |
Pour introduire le nombre dérivé, on peut, par exemple, montrer par une étude graphique avec un traceur de courbe et une étude numérique avec un tableur que la fonction x --> 2x - 1 est une approximation affine de x --> x2 au voisinage de 1. La droite d'équation y = 2x - 1 est alors la tangente à la courbe au point de coordonnées (1 ; 1). |
| Le nombre dérivé est le coefficient directeur ou la pente de la tangente ; notation f'(xA) |
Savoir que le nombre dérivé en xA est le coefficient directeur de la tangente à la courbe au point A de coordonnées (xA ; f(xA)). Connaître la notation f'(xA) |
Toute notion de limite est hors programme. On parle de pente uniquement lorsque le repère cartésien est orthonormal. Exemple : coût marginal. |
1. L’imagiciel Géoplan proposé permet de faire pivoter une droite autour d’un point de la représentation graphique d’une fonction afin d’amener cette droite à approcher au plus près au voisinage du point choisi la représentation graphique de la fonction.
L’utilisation du zoom sur le point choisi permet de vérifier que l’on a déterminé le meilleur coefficient directeur possible.
L’imagiciel propose de plus le choix entre 4 fonctions f1, f2, f3 et f4 définies par :
f1 : x--> x2
f2 : x--> 9 – x2
f3 : x--> x3
f4: x--> 8 – x3
Les commandes :
Les touches 1, 2, 3 ou 4 permettent de choisir l'une des quatre fonctions.
La touche X permet ensuite à l'aide des flèches de déplacer le point M mobile sur la courbe.
La touche D permet de faire afficher une droite (d) passant par M ainsi que son équation réduite.
La touche M permet ensuite à l'aide des flèches du clavier de modifier la valeur du coefficient directeur m de la droite (d).
La touche Z permet d'effectuer un zoom avant sur le point M (de rapport 1,2)
La touche E permet d'effectuer un zoom arrière sur le point M (de rapport 1 / 1.2)
Pour zoomer en continu tenir la touche correspondante enfoncée
La touche 0 (zéro) permet de donner à l'abscisse du point M la valeur 1 et au coefficient directeur m la valeur 1.
2. D’autre part le fichier tableur permet, par le calcul et sur la représentation graphique, de vérifier qu’au voisinage d’un point choisi, une droite donnée « approche au plus près » la représentation graphique de la fonction.
Dans ce fichier tableur, il est possible sur la feuille de calcul de modifier :
- l'abscisse du point M (son ordonnée est recalculée immédiatement suivant la fonction utilisée) ;
- le coefficient directeur de la droite passant par M (son ordonnée à l'origine sera alors recalculée automatiquement) ;
- le pas de variation des valeurs de x ; la liste en est modifiée de façon à couvrir un intervalle centré sur l'abscisse du point M.
Le fichier tableur permet de travailler sur les quatre fonctions utilisées par l’imagiciel Géoplan.
Les fichiers tableur et Géoplan proposés :
|
|
Excel |
OpenOffice StarOffice |
| Fichier Géoplan |
nbr_deri.g2w |
nbr_deri.g2w |
| Fichier tableur |
nbr_deri.xls |
nbr_deri.sxw |
| Téléchargement (Fichiers tableur et Géoplan) |
Fichier compressé (10 Ko) |
Fichier compressé (26 Ko) |
Statistiques et utilisation de sites
de statistiques ![]()
Il a été précisé lors des journées inter-académiques de Toulouse que :
« Les statistiques à une variable sont à entretenir en Terminale. »
Les calculs des différents paramètres d’une série statistique se feront à l’aide de la calculatrice ou du tableur en respectant les définitions du G.E.P.S. du 22/12/2000 :
Quantiles et diagrammes en boîtes (GEPS de mathématiques, 22 décembre 2000)
Les calculatrices ne respectant pas toujours les définitions du G.E.P.S., vous trouverez dans le document « Compléments Calculatrices » des programmes de statistiques pour TI et Casio donnant les indicateurs conformes à ces définitions ainsi que des programmes pour TI et Casio permettant de faire du lissage par moyennes mobiles (ordre pair et impair avec définitions correctes) ; ces programmes sont dus à notre collègue Alain CHARLES du Lycée de Sarlat (24).
Télécharger le document « Compléments Calculatrices » (fichier PDF : 50 Ko)
Afin de travailler avec des données plus proches des domaines étudiés dans les disciplines technologiques et pour montrer l’intérêt du tableur lors du traitement de grandes quantités de données il est intéressant de se tourner vers des sites officiels présentant des données statistiques.
Une grande majorité de ces sites proposent de récupérer les données sous forme de fichiers Excel (extension .xls) ; de tels fichiers sont ouverts sans aucun problème par le tableur OpenOffice. Sur le site de l’INSEE, les résultats du recensement de 1999 ne pourront être récupérés sous forme de fichiers (extension .csv : utilisables avec n’importe quel tableur) qu’à la condition d’utiliser comme navigateur Internet Explorer sur une machine sous Windows Xp.
Une sélection de sites :
http://www.insee.fr (le site de l’INSEE (données tableur).
http://www.alternatives-economiques.fr/indicateurs/ (tableaux statistiques au format pdf)
http://www.insee.fr/fr/liens/liens_france.htm (page de liens vers les différents sites statistiques français
http://library.ined.fr/ABSYS/ressource/ressources.htm (cette page propose une sélection de ressources statistiques démographiques disponibles sur les sites Internet d’organismes officiels et de quelques sites indépendants, retenus pour leur intérêt et la qualité de leurs sources).
http://unstats.un.org/unsd/methods/inter-natlinks/sd_natstat.htm (National Statistical Offices - data sources and links, site des nations unies).
http://www.oecd.org/statsportal/0,2639,fr_2825_293564_1_1_1_1_1,00.html (portail statistique de l’OCDE ; nombreux tableaux et graphiques sous Excel).
Réalisation de diagrammes en boîtes ![]()
Les diagrammes en boîtes apparaissent dans le programme de la classe de première.
| Contenus |
Capacités attendues |
Commentaires |
| Étude de séries de données statiqtiques à une variable |
|
|
| Histogrammes, diagrammes en boîte, en secteur ou en bâtons. |
Interpréter un diagramme donné. Construire un diagramme à partir d'un tableau de valeurs ; Choisir un graphique adapté. |
|
Le projet de document d’accompagnement (page 17) précise :
« Le diagramme en boîte (dit aussi « diagramme de Tuckey », « boîte à moustaches » ou « boîte à pattes ») peut s'arrêter aux valeurs extrêmes ou aux derniers déciles selon les attentes précisées dans l'énoncé. Il permet des comparaisons visuelles rapides entre plusieurs séries statistiques, tant en ce qui concerne la tendance centrale que la dispersion. »
On pourra utiliser l’outil tableur proposé sur le site académique (pour les différents modèles de tableur) :
http://mathematiques.ac-bordeaux.fr/profplus/logiplus/tableur/moustaches/tukey_intro.htm
ou la calculatrice en s’aidant du document « 36 élèves, 36 calculatrices » et des compléments pour les diagrammes en boîtes qu’il est possible de télécharger :
http://sierra.univ-lyon1.fr/irem/tlcharge1.htm
pour les calculatrices :
| Casio graph 100 Casio graph 25 Casio graph 35, 65... |
TI 80 TI 82 TI 83 TI 86 TI 89, 92 |
HP 38, 40 Sharp |
Exemples d’activités avec la calculatrice ![]()
Le travail de simulation entrepris en classe de seconde est à poursuivre en classe de première STG.
| Contenus |
Capacités attendues |
Commentaires |
| Expérimentation et simulation |
Comparer une fréquence observée à une probabilité théorique. Dans des situations élémentaires, reconnaître et réinvestir des situations de probabilité issues de différents types de tirages aléatoires. |
En parallèle avec des activités expérimentales concrètes, on utilise des tables de nombres aléatoires, la calculatrice ou le tableur pour simuler ces expériences. Exemples : tirages successifs avec ou sans remise. On exclut les tirages simultanés. |
L’utilisation de la programmation de la calculatrice peut d’une part inciter les élèves « réfractaires » à effectuer l’achat d’une machine permettant de réaliser les travaux demandés en classe et d’autre part raccrocher par le biais de la programmation certains élèves « allergiques » aux mathématiques.
Le travail de programmation pour obtenir des simulations devra être introduit très progressivement et faire l’objet d’un travail hors du temps de la classe ; en demandant aux élèves de collationner les résultats des simulations obtenues, le professeur obtiendra un nombre intéressant d’échantillons différents.
Ce travail pourra s’inspirer des ouvrages publiés par l’Irem de Paris-Nord :
http://www-irem.univ-paris13.fr/Publications.htm
Simulations et Statistiques en Seconde
Simulations d’expériences aléatoires
qui proposent différentes simulations à réaliser ainsi que les programmes pour les modèles courants de calculatrices TI et Casio.
Les activités proposées dans l’atelier :
(a) Réaliser un générateur de nombres aléatoires :
télécharger le document « Un générateur de nombres aléatoires » (fichier pdf : 19 Ko)
(b) La fonction « Random » de la calculatrice ; simuler le lancer d’un dé :
télécharger le document « La fonction Random de la calculatrice » (fichier pdf : 18 Ko)
(c) Réaliser une simulation : projet de document d’accompagnement (page 22)
« Un jeu consiste à jeter deux dés réguliers indépendants. On gagne si la somme des points dépasse strictement 10. On cherche la probabilité p de gagner.
– On peut, en premier lieu, rechercher une valeur approchée de cette probabilité en simulant, à l'aide de la calculatrice ou du tableur, un certain nombre de réalisations de cette épreuve.
– Dans un second temps, on peut rechercher la valeur exacte par le raisonnement, en construisant un arbre par exemple
– Les résultats des deux démarches sont-ils compatibles ? »
télécharger le document « Lancer de deux dés »
(organigramme et programmes pour Casio et TI ; fichier pdf : 20 Ko)
Suites arithmétiques et géométriques ![]()
Les suites arithmétiques et géométriques apparaissent dans les programmes des classes de première et de terminale avec des capacités attendues différentes.
Classe de première S.T.G. :
| Contenu |
Capacités attendues |
Commentaires |
| Suites arithmétiques et géométriques |
|
|
| Suites arithmétiques définies par un+1 = un + a et une valeur initale u0 ou u1.
Suites géométriques de raison positive définies par un+1 = b un et une valeur initale positive u0 ou u1. |
Reconnaître, dans une situation « concrète » une suite arithmétique (variation absolue constante) ou une suite géométrique (variation relative constante). |
Le tableur est un outil particulièrement adapté à l'introduction des suites arithmétiques et géométriques. L'objectif est de décrire des situations discrètes simples, autant que possible choisies en lien avec les autres enseignements (intérêts simples, intérêts composés, évolution ou actualisation d'un capital, évolution démographique,...) Donner les deux notations un et u(n). |
| Formule explicite
|
Claculer le terme de rang n en fonction du terme initial et de la raison. |
Le tableur permet de comparer formule de récurrence et formule explicite. Les suites géométriques offrent un terrain prpice à la consolidation des connaissances sur les puissances. |
| Représentation graphique |
Exploiter ou réaliser une représentation graphique d'une suite arithmétique ou d’une suite géométrique. |
Pour une suite arithmétique, l'alignement des points est démontré en explicitant la fonction affine sous-jacente. |
Classe terminale S.T.G. (toutes spécialités) :
| Contenu |
Capacités attendues |
Commentaires |
| Suites arithmétiques et géométriques. Comparaison de suites |
Dans le cadre de la résolution de problèmes, comparer deux suites géométriques, une suite géométrique et une suite arithmétique. |
Pour les suites géométriques, on se limite aux suites à termes positifs. Pour certaines résolutions, le tableur grapheur est indispensable. |
| Somme de termes consécutifs. |
Calculer la somme de n termes consécutifs d’une suite arithmétique ou géométrique |
Exemples : emprunt à annuités constantes, valeur actuelle d'une suite d'annuités constantes. |
Il est nécessaire que les élèves sachent utiliser correctement leur calculatrice pour travailler sur les suites afin de vérifier certains résultats du cours et/ou de répondre rapidement à certaines questions (par exemple : « quel est le terme de la suite qui est supérieur à … »)
Activité proposée dans l’atelier (projet de document d’accompagnement : page 14) :
« Un jeune travailleur a le choix entre deux contrats d’embauche. Dans le premier contrat, on lui propose un salaire mensuel brut de 1 500 € qui sera augmenté tous les ans de 60 €. Dans le second, on lui propose un salaire de 1 450 € qui sera augmenté tous les ans de 4,5 %.
Cette situation peut conduire à la comparaison des salaires annuels obtenus avec ces deux contrats pendant les premières années, puis, à prolonger l’étude à l’aide d’un tableur.
Par exemple :
– en déterminant au bout de combien d’années le salaire aura doublé selon le contrat choisi ;
– en déterminant au bout de combien d’années le second contrat donne un salaire annuel plus grand que celui obtenu avec le premier contrat ;
– en calculant les sommes respectives des salaires gagnés avec le premier et le second contrat.
Une activité de niveau première si on utilise le tableur (ou la calculatrice) ou de niveau terminale en utilisant les formules de somme. »
Télécharger le document « Suites » (fichier pdf donnant la marche à suivre sur TI et Casio : 24 Ko)
Utilisation de la calculatrice en
tableur ![]()
Une calculatrice permet de simuler un certain nombre d’opérations réalisables avec un tableur en travaillant sur les listes.
Néanmoins, à part les TI 89, 92, Voyage, elle ne conserve pas trace de la formule utilisée pour créer la liste : toute modification de cette formule passera par une nouvelle saisie de la formule.
Il n’est pas possible dans une liste de calculer un élément à partir d’autres éléments de cette même liste, par contre on peut créer une liste en utilisant des éléments placés sur la même ligne dans d’autres listes existantes.
Remarque :
Les TI 83 Plus, TI 89, … peuvent utiliser un véritable tableur vendu 15 € pour la TI 83 Plus ou 75 € en licence établissement.
Le professeur pourra s’aider du document « 36 élèves, 36 calculatrices » et des compléments pour l’utilisation de la calculatrice comme tableur qu’il est possible de télécharger :
http://sierra.univ-lyon1.fr/irem/tlcharge1.htm
pour les calculatrices :
| Casio graph 100 Casio graph 25 Casio graph 35, 65... |
TI 80 TI 82 TI 83 TI 86 TI 89, 92 |
HP 38, 40 Sharp |
Les activités proposées dans l’atelier pour les calculatrices à listes :
Télécharger le document : « Le tableur de la calculatrice » (fichier pdf : 18 Ko).
Éclairage sur le vocabulaire économique ;
exemples d’activités transdisciplinaires ![]()
L’objectif de l’atelier est d’apporter un éclairage sur les notions économiques mentionnées dans les programmes et répondre en particulier aux questions suivantes :
● Quelles sont les articulations avec les programmes d’économie-gestion ?
● Quel est le rôle du professeur de mathématiques ? Jusqu’où va-t-il ?
● Quelles doivent être les exigences du professeur de mathématiques sur ces notions (vocabulaire, formules, démarches…) ?
● Quels type d’exercices et activités peut-il proposer aux élèves pour combiner la faisabilité par les élèves et la cohérence avec la réalité du monde économique et financier ?
Le document d’accompagnement est riche en explications concernant ces notions et fournit de nombreuses activités à mener en classe avec les élèves. L’atelier souligne la nécessité d’une étroite collaboration avec les professeurs d’économie-gestion (vocabulaire, méthodes, pratiques) ; le cours de mathématiques ne devient pas un cours de gestion, mais s’articule avec celui-ci : il se propose d’expliquer les notions et d’établir des formules, qui seront utilisées dans le cours de gestion, favorisant ainsi la motivation des élèves. Le vocabulaire économique ne peut être exigé dans le cours de mathématiques et sera explicité lors de l’examen.
Les notions abordées dans cet atelier :
1. Taux et Indices
télécharger le document « Taux Indices » (fichier pdf : 29 Ko).
2. Intérêts
télécharger le document « Intérêts » (fichier pdf : 23 Ko).
3. Suites d’annuités constantes
télécharger le document « Annuités Constantes » (fichier pdf : 19 Ko).
4. Emprunts
télécharger le document « Emprunts » (fichier pdf : 23 Ko).
5. Multiplicateur d’investissement
télécharger le document « Multiplicateur d’investissement » (fichier pdf : 16 Ko).