Liaison Troisième / Seconde |
|
| |
Zone d'Animation Pédagogique d'Arcachon
Réunion du 16 octobre 2002 au lycée Nord Bassin d'Andernos (Gironde)
Équipe académique Mathématiques |
| |
Cette réunion, organisée à la demande des chefs d'établissement
de la ZAP d'Arcachon, a permis à une cinquantaine de professeurs de Mathématiques
des collèges et lycées de cette zone de se rencontrer et d'échanger sur leurs
pratiques pédagogiques autour du thème de la liaison troisième / seconde.
L’animation de la journée était assurée par Monsieur Xavier Sorbe,
IA-IPR de Mathématiques de l'académie de Bordeaux, ainsi que par des membres
de l'équipe académique Mathématiques.
Monsieur Pernet, proviseur du lycée Nord Bassin d'Andernos où se
déroulait la réunion, soulignait dans son mot d'ouverture que le renforcement
de la liaison troisième / seconde s'inscrivait, avec l'accent mis sur l'accueil
et le suivi des élèves de seconde, au cœur d'un des trois objectifs principaux
du projet d'établissement.
Monsieur Sorbe introduisait les travaux en souhaitant que cette
réunion soit l'occasion de travailler de façon décloisonnée et permette de conforter
ou d'amorcer une telle liaison, en mettant au clair les méthodes utilisées et
les objectifs à atteindre. Il précisait que, dans le but de se consacrer à des
aspects très concrets de l'enseignement, il avait été choisi de mettre en évidence tout l'intérêt
d'une liaison troisième / seconde dans le domaine du calcul littéral.
Plan de la demi-journée
— Introduction sur les objectifs d’une liaison inter cycle.
— Les moyens de communication en Mathématiques dans l'académie
(bulletin
Réciproques, liste de diffusion Listmath,
site mathématique).
— Enjeux des programmes de la sixième à la seconde ; présentation
des procédures d'aide ou de soutien et des itinéraires de découverte.
Plus précisément, évolution de l’enseignement du calcul littéral. Problèmes
que cela pose aux élèves : étude rapide d’exemples dans les évaluations
de seconde ; remédiation.
— Travail en groupes sur le calcul littéral de la sixième à la
seconde. Synthèse.
— Pistes pour une poursuite de la liaison intercycles.
I- Introduction sur les objectifs d’une liaison inter cycle
— Permettre aux collègues de se rencontrer et d’échanger sur leurs
différentes pratiques.
— Favoriser une meilleure articulation des enseignements.
— Mettre l'accent, pour les professeurs de collège, sur les difficultés
que pourraient éprouver certains élèves au lycée, connaissant les programmes
de lycée ; cela peut aller également dans le sens d'une meilleure orientation
des élèves.
— Réciproquement, présenter aux professeurs de lycée les difficultés
que pourront éprouver certains de leurs élèves, connaissant les programmes de
collège.
— Favoriser ainsi une meilleure intégration des élèves au lycée.
II- Programmes et procédures d’aide ;
difficultés liées au calcul littéral ou algébrique.
— Examen des programmes et de leurs objectifs de la sixième à la
seconde, en ce qui concerne le calcul littéral au collège et le calcul algébrique
au lycée : mise en évidence de la continuité des programmes.
— Continuité également des procédures de soutien : deux heures
d’aide aux élèves et d’accompagnement de leur travail personnel en sixième,
une heure d’aide au travail personnel en cinquième, une heure d’aide individualisée
pour huit élèves en difficulté par classe, en seconde. Présentation aux collègues
de lycée des itinéraires
de découverte qui succèdent aux travaux croisés.
— Nécessité d'une introduction prudente et très progressive des
notions de calcul littéral au collège ; historiquement, cette notion a
été très longue à installer ; ce n’est qu’au XVIe siècle que
l’on atteint, avec François Viète, le stade de l'algèbre symbolique : désormais
les lettres sont utilisées non seulement pour représenter des quantités inconnues
mais également pour désigner des données ; il devient alors possible d'exprimer
des solutions générales de problèmes et d'utiliser l'algèbre comme outil pour
prouver des règles de calcul.
— Difficultés rencontrées par les élèves : examen des exercices
d’une page d’un cahier d'évaluation de début de seconde (l’évaluation en début
de seconde ne se fait plus, mais il demeure possible, et même conseillé, d’utiliser
les anciens cahiers pour concevoir des évaluations à distribuer au fil de l’année
et du déroulement du travail). Mise en évidence de la difficulté du passage
de «l'arithmétique » pratiquée à l’école primaire au calcul littéral en
collège ; erreurs provenant d’une mauvaise compréhension des différents
statuts de la lettre et de l’égalité, peut-être également d’un apprentissage
trop rapide, d’une suppression trop hâtive du signe «multiplié » dans certaines
écritures - du type 6(x + 5) par exemple - etc. (on pourra consulter
à ce sujet le dossier «Calcul
littéral au collège » ; idées de séquences de remédiation.
— Invitation à bien connaître les étapes du programme du collège,
pour les collègues enseignant en lycée, et ce qui est attendu en seconde pour
les collègues enseignant en collège.
III- Travail en groupes
sur le calcul littéral de la 6e à la 2e,
puis synthèse
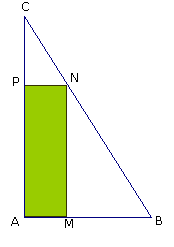
| 1. Une situation
est proposée aux collègues
On considère un triangle ABC rectangle en A.
On donne AB = 6 et AC = 12.
AMNP est un rectangle. AM est variable.
Il s’agit d’essayer d’élaborer des énoncés d’exercices
adaptés à chaque niveau (6e, 5e, 4e,
3e, 2e) à partir de ces données, plus ou moins complétées,
pour construire des situations utilisant le calcul algébrique dans ces
différents niveaux, autour de la notion d’aire ou de périmètre.
À travers ces exercices, on cherche à faire évoluer la
notion de lettre, ainsi que son statut. |
 |
2. Travail en ateliers
3. Mise en commun des travaux
3.a. Les exercices proposés par les collègues sont présentés ci-après,
de façon succincte et sans rappeler les données de départ.
| En 6e |
APNM est un
rectangle MB = 1 et AP = 2.
Calculer AM
Calculer l’aire et le périmètre du rectangle
La longueur AM et l’aire du rectangle étant données, trouver
AP.
|
| En
5e |
On
pose AM = x
Exprimer MB à l’aide de x (pour introduire "en fonction
de")
Calculer MB lorsque x = 5, x = 3,
x = 2/3.
|
| En 4e |
1) On
donne AM = 2 ; calculer CP, AP et l’aire du rectangle APNM
2) On pose AM = x ; exprimer CP et
AP à l’aide de x et vérifier pour x = 2 ; exprimer l’aire
du rectangle APNM en fonction de x et vérifier pour x = 2
3) Déterminer x pour que APNM soit un carré. Calculer
l’aire dans ce cas.
|
| En 3e |
Même version
qu’en quatrième, en ajoutant la question : quelles sont les valeurs
possibles de x ?
Une autre version possible :
Exprimer AP en fonction de x. Déterminer le périmètre
du rectangle et tester s’il peut prendre une valeur donnée. Exprimer l’aire
du triangle MNB en fonction de x, et trouver pour quelle valeur de x l’aire
vaut 4, en guidant les élèves vers une "équation produit".
|
| En 2e |
On pose AM = x
On considère la fonction A qui à tout x associe l’aire
du rectangle APNM. Exprimer A(x).
On étudie la fonction A : ensemble de définition,
étude des variations en guidant les élèves, tableau de valeurs et représentation
graphique que l’on exploitera. |
3.b. La mise en commun des exercices élaborés par chaque groupe
permet de dégager les idées principales et surtout les différentes
étapes dans l’utilisation de la lettre.
| En 6e |
Employer seulement
une formule avec substitution (donner aire ou périmètre et longueur, trouver
la largeur)
Compléter une "égalité
à trou"
|
| En 5e |
Introduire
la notion de variable (exprimer "en fonction de")
Calculer avec différentes valeurs de x.
Tester si une égalité (ou une inégalité simple) est vraie
Résoudre des équations simples en utilisant uniquement
le sens des opérations
|
| En 4e |
Développer,
réduire une expression.
Résoudre une équation du premier degré.
La lettre peut prendre différents
statuts : elle peut être une variable à laquelle on donne
différentes valeurs, une inconnue,…
|
| En 3e |
Utiliser les
factorisations et les égalités remarquables.
Encadrer x, poser le problème de la validité d’une
solution.
Résoudre une "équation
produit"
|
| En 2e |
Utiliser les
connaissances du collège à travers des situations de problèmes.
Étudier des fonctions en utilisant les fonctions de référence :
variations, tableau de valeurs.
Tracer des représentations graphiques.
Exploiter ces représentations |
IV- Prolongement
Nous proposons ci-après un exercice qui peut être posé en troisième
en enlevant la dernière question, et qui peut être également posé en seconde
en changeant éventuellement certaines consignes et en les adaptant un peu. Le
tableau de valeurs permet aux élèves de voir «bouger » l’aire quand x varie,
et de mieux sentir la notion de fonction ; c’est une notion difficile,
dont la mise en place débute en troisième et se poursuit tout au long du lycée.
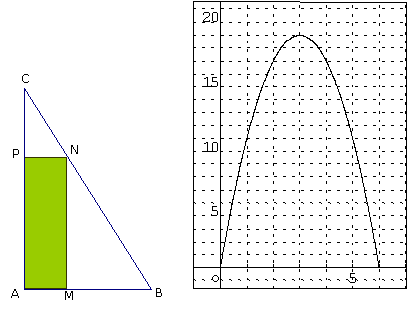
ABC est un triangle rectangle en A tel que AB = 6 cm et
AC = 12 cm. Le point M décrit le segment [AB]. Le réel x désigne,
en cm, la longueur AM. On construit le rectangle AMNP où N appartient à [BC]
et P appartient à [AC]. On appelle f(x) l’aire, en cm², du rectangle AMNP. On
admet que (C) est la courbe représentative de f dans le repère (O, I,
J) ou 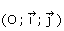 .
.
1. Faire une figure, placer le point M tel que AM = (2/3)AB,
tracer le rectangle AMNP et calculer son aire. Retrouver ce résultat sur le
graphique en laissant apparents les tracés utilisés.
2. Compléter le tableau suivant :
| Longueur
AM
x |
0 |
1 |
2 |
2,5 |
3 |
4 |
6 |
| Aire
du rectangle
f(x) |
0 |
10 |
|
|
|
|
|
3. Pour quelle position de M l’aire du rectangle AMNP semble-t-elle
maximale ? Qu’avez-vous utilisé pour répondre : le graphique, la figure
ou le tableau ?
4. Exprimer en fonction de x l’aire f(x) du rectangle AMNP.
5. Vérifier que f(x) = 18 – 2 (x - 3)². En déduire alors
que f(x) £ 18.
V- Pistes pour une poursuite de la liaison inter cycles
La liaison inter cycles ne consiste pas qu’en réunions ! Parmi ce
qui se fait ou ce que l’on pourrait imaginer entre un lycée et le ou les collèges
qui «l'alimentent », citons :
— les échanges autour des objectifs des programmes, des contenus,
des méthodes, des exigences, des orientations ;
— les échanges sur les contenus des anciens cahiers d’évaluation
de seconde ;
— les échanges de devoirs, les corrections communes ou croisées,
l’élaboration commune de devoirs ;
— la participation croisée aux conseils de classe (troisième -
seconde) ;
— le retour des bulletins de seconde vers le collège d’origine
de l’élève ;
— les projets communs : expositions, sorties, rallye mathématique ;
pourquoi pas des "défis" entre classe de 3e et classe de
2e ? ;
— et enfin les visites croisées de classes : un collègue de
collège ouvre sa porte à un collègue de lycée et réciproquement. Ceux qui l'ont
fait en témoignent : on prend mieux la mesure de ce que vivent nos élèves et
on donne ainsi sa vraie dimension au travail inter cycles !


 .
.