2. Les frises

Équipe académique mathématiques C. Drouin Bordeaux, novembre 2002 sommaire       parcourir le dossier

Les frises constituent un domaine mathématique relativement simple qui permet de s'initier aux pavages et d'employer l'outil "isométries", tout en présentant un aspect artistique intéressant. Elles sont une bonne introduction aux pavages bipériodiques (fiches 3.1 et suivantes), qui mettent en jeu les mêmes concepts mathématiques, mais de façon plus complexe (plus spectaculaire aussi).

Cette fiche indique comment analyser, et surtout réaliser, des frises. Elle présente les notions mathématiques qui interviennent.

Pour aborder les frises de façon plus visuelle, plus plaisante et moins théorique, on peut commencer par consulter les paragraphes C. et D. , en revenant sur les définitions dans un second temps.

Au sommaire de cette page

A. Définitions (Concept de Frise. Ensemble translaté de base : rectangle, parallélogramme.)

B. Isométries d'une frise (Isométries du dessin. Rectangle minimal. Ensemble translaté adapté.)

C. Réalisation d'une frise simple

D. Classification des frises (Théorème de classification des frises. Rectangle minimal.)

E. Construction d'une frise plus éléborée

A. Définitions

Bande

On appelle bande du plan la zone du plan comprise entre deux droites parallèles.

On suppose désormais choisie une bande B du plan.

Dessin

On considère ici qu'un dessin dans la bande B n'est autre qu'un sous-ensemble D de cette bande. Dans le cas par exemple d'un dessin en noir et blanc, on peut considérer que D est l'ensemble des points de la bande en noir, l'ensemble complémentaire de D dans B étant en blanc.

Frise

Soit D un dessin dans une bande B, c'est-à-dire un sous-ensemble de B. On dit que D est une frise de B si il existe un vecteur u tel que :

* u est un vecteur directeur des deux droites frontières de la bande.

* D est invariant par la translation de vecteur u, c'est-à-dire : tu(D) = D.

* Si D est invariant par une translation de vecteur v, alors v est de la forme v = k.u, k étant un entier relatif. Autrement dit, u est un des deux vecteurs non-nuls de norme minimale des translations laissant D invariant. On dit que u est un  vecteur minimal de la frise.

On peut exprimer de façon concrète le fait que D soit invariant par la translation de vecteur u : si on décalque D, et si on fait glisser le calque suivant le vecteur u , on peut de nouveau faire coïncider le dessin de D sur le calque avec D.

Décor

On peut aussi vouloir donner de l'importance aux couleurs de la figure. Nous parlerons alors de décor de la bande.

Dire qu'un décor est invariant par une isométrie f du plan, c'est dire que toute partie P du décor se transforme par f en une partie f(P) ayant mêmes formes et mêmes couleurs.

Définition précise d'un décor

Attention

Une isométrie f peut fort bien laisser les dessins (les formes) invariants et ne pas respecter les couleurs. Quand on recherche les isométries d'une figure, il faut spécifier s'il s'agit du décor coloré ou du seul dessin.

Analyser une frise

Il convient d'abord de repérer un vecteur minimal de la frise.

Ensemble translaté de base d'une frise

Il s'agit d'une partie E du plan, fermée (c'est-à-dire contenant sa frontière), connexe (c'est-à-dire d'un seul tenant), ayant la propriété suivante :

Les translatés de E par les translations de vecteurs k.u avec k entier relatif, recouvrent totalement la bande B, sans laisser de vide, et sans empiéter l'un sur l'autre, sinon par leurs frontières.

Autrement dit, les translatés de E réalisent un pavage de la bande, invariant par les mêmes translations que le dessin lui-même.

Si l'on veut se rappeler ce qu'est un pavage, et ce qu'est l'invariance d'un pavage par une isométrie (ce qui n'est pas essentiel pour la suite), voir la fiche 1 "Généralités sur les Pavages".

Remarques

¤ Il est toujours possible et souvent intéressant de considérer un parallélogramme translaté de base ou un rectangle translaté de base qui sont des ensembles translatés de base de forme particulière.

Il suffit de choisir un parallélogramme (ou un rectangle) dont deux côtés sont inclus dans les droites frontières de la bande et supportent, de plus, un vecteur minimal de la frise.

¤ La partie du dessin tracée dans un tel parallélogramme de base n'a généralement pas une forme agréable. Souvent, le motif même du pavage, ou une réunion de motifs, fournit un ensemble translaté de base plus esthétique et plus commode.

¤ Tous les ensembles translatés de base ont la même aire.

Analyse

Repérer de tels ensembles translatés de base sur les exemples présentés.

B. Isométrie d'une frise

1. Outil mathématique nécessaire : les isométries du plan

- Translations

- Rotations (dont symétrie centrale)

- Réflexions ( c'est-à-dire symétries orthogonales)

- Éventuellement : réflexion glissée.

On appelle réflexion glissée la succession d'une réflexion s et d'une translation tw dont le vecteur directeur dirige l'axe de la réflexion. Mathématiquement, l'isométrie résultante est appelée composée des isométries s et tw, et notée tw o s.

2. Isométrie d'une frise

On dit qu'une transformation f est une isométrie de la frise D si f laisse invariant aussi bien la bande B que le dessin D. Autrement dit si on a à la fois : f(B) = B et f(D) = D.

Analyser un dessin

Repérer les isométries d'une frise.

3. Isométrie possibles d'une frise

- Si c'est une rotation, ce ne peut-être qu'une symétrie centrale, le centre se trouvant sur l'axe de symétrie de la bande.

- Si c'est une symétrie orthogonale, son axe est soit l'axe de symétrie de la bande, soit une droite perpendiculaire à cet axe de symétrie.

- Si c'est une réflexion glissée, son axe est l'axe de symétrie de la bande.

Activité

Démontrer ce résultat

On pourra pour cela admettre que si une isométrie f transforme la bande B en B elle-même, alors f transforme la frontière de B en la frontière de B elle-même. Soient d' et d" les deux droites qui constituent la frontière de B, on a alors : f( d ' U d " ) = d ' U d ".

Analyser une frise

Tracer les axes de symétrie, placer les centres des symétries centrales laissant la frise invariante ; éventuellement, définir les symétries glissées laissant la frise invariante.

On obtient aussi un ensemble de points et d'axes qui est essentiel pour l'étude de la frise et qui en est comme le "squelette". On appellera cet ensemble la trame du dessin.

4. Ensemble minimal d'une frise

Il s'agit d'une partie M de la bande B telle que si l'on prend tous ses ensembles transformés f(M) par toutes les isométries f laissant la frise invariante, les ensembles
f(M), tous distincts, recouvrent le plan, sans empiéter l'un sur l'autre, sinon éventuellement à leurs frontières.

Autrement dit, les ensembles f(M) réalisent un pavage de la bande.

On appelle motif minimal l'intersection du dessin, ou bien du décor, avec l'ensemble minimal.

Remarque

Il est toujours possible, et souvent intéressant, de considérer un parallélogramme minimal ou un rectangle minimal qui sont des ensembles minimaux de formes particulières.

Analyser un dessin

Repérer un ensemble minimal d'une frise

5. Ensemble translaté adapté d'une frise

Un ensemble translaté adapté pour un dessin D qui est une frise est un ensemble translaté de base de D qui a, de plus, la propriété d'être constitué d'un ensemble minimal M et d'images de M par certaines isométries de la frise.

L'intérêt d'un ensemble translaté adapté est qu'il fait apparaître certaines des transformations de la frise : symétries centrales, axiales ou glissées.

Analyser un dessin

Repérer un ensemble translaté adapté d'une frise.

C. Construction d'une frise simple (simplement translatée)

L'exemple qui suit a été réalisé avec le logiciel Cabri. On se sert de façon essentielle de l'outil "polygone" de Cabri.

On souhaite réaliser une frise de voiliers, frise du type le plus simple : F1, simplement translaté (voir le paragraphe suivant).

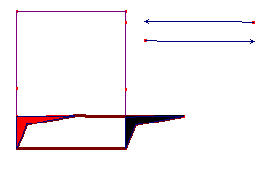
On part donc du rectangle qui est le rectangle translaté de base (et aussi, en l'occurence, le rectangle minimal). On commence à dessiner la coque du voilier. Si on ajoute une proue (en noir) hors du rectangle minimal, la partie translatée correspondante (en rouge), doit être enlevée du dessin, ce qui modifie l'arrière du bateau
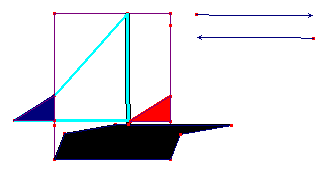
Occupons nous maintenant de la voile. Si une partie (en bleu) de la voile déborde du rectangle minimal, il faudra ôter (en rouge) sa translatée.
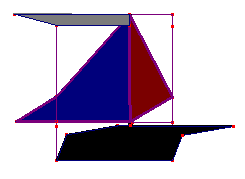
En tenant compte de cette partie supprimée, on complète la figure par un foc et un pavillon qui va jusqu'au mat suivant. Ca y est, on a notre motif minimal (et translaté). Reste seulement à le reproduire par translation pour obtenir une frise des plus simples (de type F1).

Si vous êtes intéressé par ce type de construction de frises, consultez le paragraphe E ci-dessous. Cependant, pour réaliser de belles frises, il faut avoir quelques notions théoriques, fournies par le paragraphe D suivant.

D. Classification des frises

1. Théorème de classification

Les frises se répartissent selon les sept types suivants, qui correspondent bien à leur aspect visuel (on note G l'ensemble des isométries de la frise, et d l'axe de symétrie de la bande) :

- G ne comprend que des translations (type F1)

- G ne comprend que des translations et des symétries centrales dont le centre est sur d (type F2)

- G ne comprend que des translations et la symétrie orthogonale d'axe d (type F1m)

- G ne comprend que des translations et des symétries orthogonales d'axes perpendiculaires à d (type Fmm)

- G ne comprend que des translations et des symétries glissées d'axe d (type F1g)

- G ne comprend que des translations, des symétries centrales et des symétries orthogonales d'axes perpendiculaires à d (type Fm2)

- G ne comprend que des translations, la symétrie d'axe d, des symétries orthogonales d'axes perpendiculaires à d et des symétries centrales dont le centre est sur d (type F4)

Dans tous les cas, la disposition relative des axes et/ou des centres de symétrie peut être parfaitement précisée à l'aide du vecteur u d'une translation minimale.

Par exemple, dans le cas F2, les symétries centrales ont toutes leur centre sur d. De plus, sur cette droite, on passe d'un des centres au suivant par la translation de vecteur 1/2.u . De telles précisions peuvent être apportées pour tous les types de frises.

Activité mathématique

Composer entre elles plusieurs isométries laissant la frise invariante ; démontrer le théorème de classification.

Prérequis : savoir que l'ensemble des isométries d'une frise constitue un groupe.

2. Rectangle minimal pour chacun des types de frises

Soit pour analyser, soit surtout pour construire un dessin de type donné, il est utile, voire indispensable, de considérer un rectangle minimal et un rectangle translaté adapté de cette frise. Pour la définition de ces ensembles voir les paragraphes A et B ; pour l'utilisation graphique de ces ensembles, voir le paragraphe E.

On donne ci-dessous un rectangle minimal pour chacun des types de frises et on indique comment passer au rectangle translaté adapté correspondant.

- Dans le cas du type de frise F1 on peut prendre comme rectangle minimal un rectangle translaté de base, c'est-à-dire un rectangle dont deux côtés sont inclus dans les droites frontières de la bande, et, de plus, supportent un vecteur minimal de la frise. On peut aussi considérer un simple parallélogramme de base.

- Dans chacun des types de frise Fmm, F2, Fm2, on peut prendre comme rectangle minimal un rectangle dont deux côtés sont inclus dans les droites frontières de la bande, les deux autres côtés étant chacun soit le support d'un axe de symétrie de la frise, soit un segment contenant un centre de symétrie. On obtient alors un rectangle translaté de base, adapté, en doublant le rectangle minimal par symétrie (axiale ou centrale, c'est selon).

- De même, pour le type de frise F1g, on peut prendre comme rectangle minimal un rectangle dont deux côtés sont inclus dans les droites frontières de la bande et portent la moitié du vecteur minimal. On obtient alors un rectangle translaté de base, adapté, en doublant le rectangle minimal par la symétrie glissée.

- Pour le type de frise F1m, on peut prendre comme rectangle minimal un rectangle dont l'un des côtés est inclus dans un des bords de la frise et un autre dans l'axe d de la bande, les autres côtés supportant un vecteur minimal. On obtient alors un rectangle translaté de base, adapté, en doublant le rectangle minimal par la symétrie d'axe d.

- Pour le type de frise F4, on peut prendre comme rectangle minimal un rectangle dont l'un des côtés est inclus dans un des bords de la frise, et un autre dans l'axe d de la bande, les deux autres côtés portant des axes de symétrie de la courbe, perpendiculaires à d et consécutifs. On obtient alors un rectangle translaté de base, adapté, en doublant tout d'abord le rectangle minimal par la symétrie d'axe d, puis en doublant de nouveau le rectangle ainsi obtenu grâce à une symétrie par rapport à l'un des autres côtés du rectangle minimal.

L'utilité de ces ensembles est l'analyse, mais surtout la construction de frises.

E. Construction d'une frise élaborée (Type F1g)

Voici un exemple de construction d'une frise plus élaborée, à partir de son type.

On choisit d'abord son type, d'après la classification du paragraphe D, par exemple, ici, F1g : la frise sera invariante par des translations, mais aussi par un glissage ayant pour axe l'axe de la bande, et de vecteur la moitié du vecteur minimal.

Le rectangle minimal est fondamental pour réaliser une frise un peu élaborée.

Le paragraphe D nous indique que le rectangle minimal a des côtés qui supportent la moitié d'un vecteur minimal, et que l'on obtient un rectangle translaté de base, adapté, en prenant le rectangle minimal et en le copiant par glissage.

Pour changer un peu, la bande de la frise sera verticale.

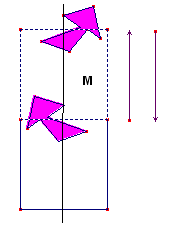
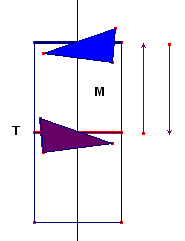
Sur la première figure,ci-contre, M désigne le rectangle minimal. Pour visualiser le glissage, on a dessiné une flèche et son image par le glissage. Le grand rectangle est le rectangle translaté de base.
Pour réaliser un dessin esthétique, il est important de savoir que les bords opposés du rectangle minimal se recollent de la façon qu'évoque la figure ci-contre : la frontière en trait bleu épais se colle sur celle en trait rouge, avec une inversion de sens signalée par le fait que la flèche bleue se colle sur la flèche violette.

L'exemple qui suit a été réalisé avec le logiciel Cabri.

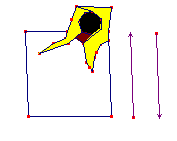
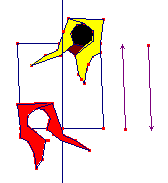
On souhaite dessiner une "pile" d'acrobates telle que la tête de l'acrobate inférieur s'emboîte entre les jambes de l'acrobate supérieur, suivant le recollement du rectangle minimal décrit plus haut (figure de gauche ci-dessous).

Mais alors les jambes jaunes vont venir se copier en rouge par glissage, et fournir celles de l'acrobate inférieur, dont la tête est déjà dessinée (figure de droite ci-dessous).

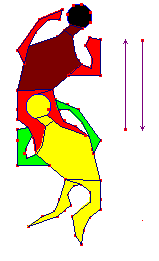
Il n'y a plus qu'à compléter l'acrobate inférieur (tronc et bras). Il constitue le motif minimal de la frise. En lui adjoignant son image par le glissage, on obtient un ensemble translaté adapté (figuratif) de la frise.

Il reste à répéter cet ensemble translaté par des translations.

On obtient une frise de type F1g. (On a ce type uniquement si on ne tient pas compte des couleurs, lesquelles ne sont ici que pour une visualisation commode).

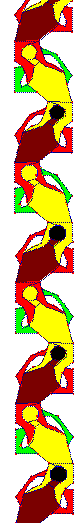
La dernière figure est réalisée en juxtaposant plusieurs des images précédentes à l'aide d'un logiciel standard de traitement d'images (par copier/coller).

Pour aller plus loin

Les pavages permettent de réaliser des dessins encore plus spectaculaires, et encore plus intéressants du point de vue mathématique.

Haut de page

sommaire       parcourir le dossier