3.2. Réalisation de dessins bipériodiques translatés

Équipe académique mathématiques C. Drouin Bordeaux, novembre 2002 sommaire  parcourir le dossier

On donne ici une méthode permettant de réaliser des pavages invariants par deux translations : on part des deux translations de base, qui correspondent à deux vecteurs de base u et v, puis on considère un parallélogramme de base : c'est tout simplement un parallélogramme dont les côtés portent les vecteurs u et v.

Au sommaire de cette page

A. Constructions simples ("art abstrait")

B. Constructions à motif simple (figuratives et plus artistiques)

A. Constructions simples ("art abstrait")

On décore tout simplement, par exemple, le parallélogramme de base de figures géométriques, en utilisant éventuellement des couleurs. Ceci peut se faire avec plus ou moins de virtuosité.

Puis on reproduit ce parallélogramme par les translations de vecteurs u et v. On pave ainsi le plan.

Pour réaliser ces constructions, on peut utiliser un logiciel de géométrie (type Cabri), ou des logiciels spécifiques pour les pavages (type Pavage, Kali ou Ornament).

B. Constructions à motif simple (figuratives et plus artistiques)

Si l'on veut obtenir des pavages plus artistiques, par exemple avec un seul dessin qui s'emboîte avec des copies de lui-même, sans laisser de blanc, il est nécessaire de procéder de façon plus fine.

Il s'agit de déformer ce parallélogramme de base, mais en faisant toujours en sorte que le motif obtenu reste invariant par les deux translations de vecteurs u et v. On obtient ainsi un ensemble translaté de base.

On peut réaliser ce motif simplement en dessinant, en translatant, en gommant.

On peut aussi découper le motif sur l'un des côtés du parallélogramme et le rajouter sur l'autre côté, après translation de vecteur u ou v (technique du puzzle).

Ces constructions peuvent être réalisées avec un logiciel de géométrie (du type Cabri).

L'ensemble translaté de base ayant été réalisé, il suffit de le déplacer par les translations de vecteurs u et v pour paver le plan.

On consultera avec profit la page 18 de l'ouvrage "Le monde des pavages" (voir la bibliographie dans la page d'introduction).

Exemple

L'exemple qui suit a été réalisé avec le logiciel Cabri. On se sert de façon essentielle de l'outil "polygone" de Cabri.

On souhaite dessiner une tête de jeune vache.

On part donc d'un parallélogramme allongé. Les deux vecteurs de base du pavage, u et v, sont portés par les côtés du parallélogramme. À gauche en haut, on fait sortir du parallélogramme ce qui sera la corne droite de la vache.

Il faut alors translater cette corne vers la droite, dans l'intérieur du parallélogramme. La forme translatée devra être découpée du parallélogramme. Son trait inférieur correspond alors à la partie supérieure du museau de la vache. Dessinons maintenant la corne gauche. Elle sort vers le haut à gauche du parallélogramme, donc il faut enlever son translaté dans le bas du parallélogramme. Dans le même mouvement, si on allonge un peu le museau à droite en bas, il faut enlever son translaté à gauche en bas.

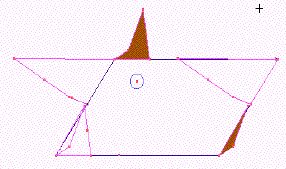De façon plus subtile (figure suivante) : enlevons un peu de matière en bas à droite du parallélogramme. Il faudra le rajouter en haut à droite, ce qui ne nous convient pas. Tout simplement, on la translate vers la gauche pour épaissir un peu la corne droite vers le haut. On rehausse aussi un peu le front devant la corne gauche, ce qui enlève son translaté en bas.
La figure suivante montre le motif (ensemble translaté de base). Il suffit alors de translater ce motif pour paver le plan.

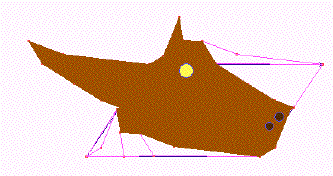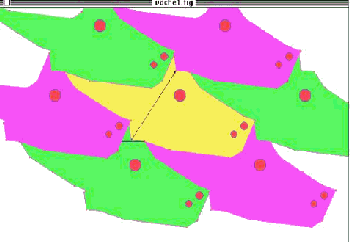
La dernière figure est réalisée en juxtaposant plusieurs des images précédentes à l'aide d'un logiciel standard de traitement d'images (par copier/coller)

Pour aller plus loin

Pour réaliser des pavages originaux et plus spectaculaires, on peut construire des pavages invariants par d'autres isométries que les translations.

Haut de page

sommaire  parcourir le dossier