3.3. Réalisation de dessins bipériodiques rotatifs

Équipe académique mathématiques C. Drouin Bordeaux, novembre 2002 sommaire  parcourir le dossier

On considère ici les dessins bipériodiques qui sont invariants par des rotations qui ne sont pas des symétries centrales.

Rappelons le théorème fondamental sur les rotations laissant invariantes un dessin (ou décor) bipériodique (voir fiche 3.1.) :

Les rotations laissant D invariant ont nécessairement pour angle, au signe près, 0°, 180° , 60°, 90°, ou 120°.

De plus, en supposant que D admette une rotation d'angle a parmi les angles ci-dessus, l'ensemble Ga des centres des rotations d'angle a laissant D invariant est constitué d'un réseau de points, aux sommets d'un pavage du plan par des triangles équilatéraux, des carrés, des parallélogrammes ou des hexagones. Le type de dessin dépend de la valeur de a.

On a également le résultat suivant (résultat 2) :

Si D est invariant par une rotation d'angle a et si Ca est l'ensemble de tous les centres des rotations d'angle a laissant D invariant, alors Ca est lui-même invariant par toutes les rotations et toutes les translations laissant D invariant.

Au sommaire de cette page

A. Classification des dessins bipériodiques rotatifs

B. Méthode de construction de dessins bipériodiques rotatifs

C. Polygones minimaux et translatés des dessins rotatifs

A. Classification des dessins bipériodiques rotatifs

Analyser le dessin

Comme toujours, pour analyser un dessin doublement périodique, il faut mettre en évidence les vecteurs des translations de base, les centres des rotations, les axes de symétrie, les réflexions glissées...

On peut également repérer les parallélogrammes de base, et mieux encore, les motifs minimaux, les polygones minimaux et les ensembles translatés adaptés construits à partir du polygone minimal ou du motif minimal.

Classification de ces dessins

Une première classe de dessins rotatifs concerne les dessins qui n'admettent comme isométries que des rotations et évidemment des translations. Cette classe regroupe les cas suivants :

• Le dessin admet comme seules isométries, en plus des translations, des rotations d'angles + ou - 120° (tiers de tours directs ou indirects). Dessin de type p3 (R3 Kangourou). Les centres des rotations sont alors au sommet d'un pavage du plan par des triangles équilatéraux dont les côtés sont des vecteurs de translations minimales.

• Le dessin admet comme seules isométries, en plus des translations, des rotations d'angles + ou - 90°(quarts de tours directs ou indirects) et 180° (symétries centrales). Dessin de type p4 (R4 Kangourou). Mis ensemble, les centres de toutes les rotations sont alors aux sommets d'un pavage du plan par des carrés. Les sommets sont alternativement centres de symétrie centrale (uniquement) et centres de quarts de tour.

• Le dessin admet comme seules isométries, en plus des translations, des rotations d'angles + ou - 60°, + ou - 120° et 180°. Dessin de type p6 (R6 Kangourou). Mis ensemble, les centres de toutes les rotations d'angles 120° sont alors aux sommets d'un pavage du plan par des triangles équilatéraux. Il en va de même du sous-ensemble formé des seuls centres de rotations d'angle 60°. Si l'on prend deux de ces derniers qui soient voisins, leur milieu est le centre d'une symétrie centrale du dessin.

Une deuxième classe de dessins rotatifs concerne les dessins qui admettent des rotations dont l'angle minimal a est un n-ième de tour, avec n = 3, 4 ou 6, qui admettent aussi des symétries axiales et qui vérifient de plus la condition : par tout centre de rotation d'angle a du dessin, passe au moins un axe de symétrie (en fait il en passe alors exactement n, avec a = 360°/n, et n = 3, 4 ou 6). Cette deuxième classe regroupe les dessins de types p3m1, p4m, p6m (Kangourou M3, M4, M6), qui correspondent respectivement à des angles minimaux de rotation de 120° (n = 3), 90° (n = 4), 60° (n = 6).

Une dernière classe de dessins rotatifs concerne les dessins qui admettent des rotations dont l'angle minimal a est un n-ième de tour, avec n = 3, 4 ou 6, et qui admet de plus des symétries axiales,mais tels que certains centres de rotations d'angle a ne soient sur aucun axe de symétrie. Cette deuxième classe regroupe les dessins de types p31m et p4g, (Kangourou M3R3, et M2R4), qui correspondent respectivement à des angles minimaux de rotation de 120° (n = 3) et 90° (n = 4).

Activités mathématiques

Pour telle ou telle catégorie de pavages rotatifs, observer et décrire la "trame" de ce pavage, c'est-à-dire les positions mutuelles des vecteurs des translations, des centres des rotations, des axes de symétrie.

Déterminer graphiquement un parallélogramme de base du pavage, et, mieux encore, un motif minimal, un polygone minimal et les ensembles translatés adaptés construits à partir du polygone minimal ou du motif minimal.

Éventuellement, démontrer que dans tel type de pavage, les positions mutuelles des vecteurs des translations, des centres de symétrie des rotations, des axes de symétrie, sont nécessairement celles qui sont constatées visuellement. (On pourra pour cela composer les diverses isométries du pavage).

B. Méthode de construction de dessins bipériodiques rotatifs

On entreprend ici de construire des dessins rotatifs.

Pour pouvoir construire soi-même un dessin, il faut faire à l'envers la démarche d'analyse précédente. On va partir cette fois du polygone minimal, des isométries du dessin et d'un ensemble adapté de base, pour arriver à dessiner le dessin de type donné.

Voici la méthode sur un exemple. Pour généraliser, voir le paragraphe suivant qui donne dans chaque cas le polygone minimal.

L'exemple traité a pour but la construction, à l'aide du logiciel Cabri-géomètre, d'un dessin de type p6 (alias dessin ; voir les caractéristiques dans le paragraphe B).

D'après le paragraphe C, le polygone minimal correspondant est (par exemple) un triangle équilatéral dont un sommet, noté I, est centre d'une rotation de 60° du pavage, tandis que les deux autres sommets sont des centres de rotations de 120°.

Dans un premier temps, on décore ce polygone minimal.

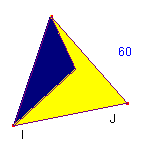
Puis l'on passe à un polygone translaté adapté correspondant, qui, comme indiqué au paragraphe C, est l'hexagone formé des images successives du polygone minimal par la rotation de centre I et d'angle 60°. Voici le polygone translaté adapté, décoré :

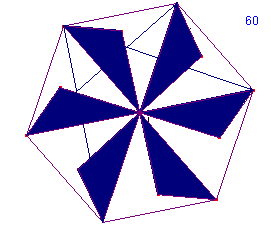
Il ne reste plus qu'à appliquer à cet ensemble transaté de base les translations minimales (dont les vecteurs sont portés par des "petites diagonales").

On obtient ainsi un dessin de type p6 où l'on voit apparaître, outre les centres de sixièmes de tour, également les centres de tiers de tour et les centres de demi-tours.

Pour plus de beauté et de virtuosité dans la construction des dessins - comme dans ceux d'Escher ou de M. Raba (voir "Le monde des pavages" cité dans la bibliographie) - et pour la réalisation de pavages figuratifs à motifs simples, il faut comprendre mieux encore les propriétés du polygone minimal. Voir pour cela la fiche 3.5 et l'ouvrage cité.

Le paragraphe qui suit donne, pour tous les types de dessins étudiées dans cette fiche, les polygones minimaux ainsi que les polygones translatés adaptés correspondants.

C. Polygones minimaux et polygones translatés des dessins rotatifs

Soit pour analyser, soit surtout pour construire un dessin de type donné parmi ceux étudiés ici, on a besoin de la forme d'un polygone minimal et de celle du polygone translaté adapté correspondant. Pour les définitions de ces concepts, voir la fiche 3.1 d'introduction aux pavages bipériodiques.

Première classe de dessins rotatifs (types p3, p4, p6)

¤ Dans le cas du type de dessin p3, on peut prendre comme polygone minimal un losange formé de deux triangles équilatéraux dont les sommets sont des centres voisins de tiers de tour laissant le dessin invariant. Soit I un sommet du losange commun aux deux triangles. En prenant le losange initial et ses deux images par les deux rotations de centre I et d'angles +120° et -120°, on obtient pour polygone translaté adapté un hexagone régulier inscriptible. Les vecteurs des translations minimales sont portés par des "petites diagonales" de cet hexagone.

¤ Dans le cas du type de dessin p4, on peut prendre comme polygone minimal un triangle rectangle isocèle dont les trois sommets sont voisins des centres des quarts de tour du dessin. Soit I le sommet principal de ce triangle rectangle isocèle. En prenant le triangle initial et ses images respectives par les rotations de centre I et d'angles +90°, 180°, -90°, on obtient pour polygone translaté adapté un parallélogramme de base qui n'est autre qu'un carré.

¤ Dans le cas du type de dessin p6, on peut prendre comme polygone minimal un triangle équilatéral dont un des sommets, I, est centre d'un sixième de tour du dessin, et dont les deux autres sommets sont des centres de tiers de tour voisins de I. En prenant le triangle initial et ses images respectives par les rotations de centre I et d'angles +60°, +120°, 180°, -120°, -60°, on obtient un hexagone régulier inscriptible pour polygone translaté adapté. Les vecteurs des translations minimales sont portés par des "petites diagonales" de cet hexagone.

Deuxième classe de dessins rotatifs (types p3m1, p4m, p6m)

¤ Dans le cas du type de dessin p3m1, on peut prendre comme polygone minimal un triangle équilatéral dont les sommets sont des centres de tiers de tour du dessin. Soit I un sommet du triangle. En doublant ce triangle grâce à une symétrie par rapport à un des côtés d'extrémité I, on obtient un losange. En prenant ce losange et ses images par les deux rotations de centre I et d'angles +120° et -120°, on obtient un hexagone régulier inscriptible pour polygone translaté adapté. Les vecteurs des translations minimales sont portés par des "petites diagonales" de cet hexagone.

¤ Dans le cas du type de dessin p4m, on peut prendre comme polygone minimal un triangle IJK rectangle isocèle en K, tel que I et J soient des centres voisins des quarts de tour laissant le dessin invariant, et K le centre d'une symétrie centrale du dessin. En doublant ce triangle par symétrie par rappport au côté [IK], on obtient un nouveau triangle rectangle isocèle, de sommet principal I. En prenant ce nouveau triangle et ses images respectives par les rotations de centre I et d'angles +90°, 180°, -90°, on obtient pour polygone translaté adapté un parallélogramme de base qui est un carré.

¤ Dans le cas du type de dessin p6m, on peut prendre comme polygone minimal un demi-triangle équilatéral dont un des sommets, I, est centre d'un sixième de tour du dessin (angle en I : 30°), dont un autre sommet, J, est un centre de tiers de tour voisin de I, (angle en J : 60°), dont le troisième sommet, K, est seulement un centre de symétrie du dessin (angle en K : 90°). En doublant ce triangle par symétrie par rappport au côté [IK], on obtient un triangle équilatéral dont un sommet est I. En prenant ce triangle équilatéral et ses images par les rotations de centre I et d'angles respectifs +60°, +120°, 180°, -120°, -60°, on obtient pour polygone translaté adapté un hexagone régulier inscriptible. Les vecteurs des translations minimales sont portés par des "petites diagonales" de cet hexagone.

Troisième classe de dessins rotatifs (types p31m, p4g)

¤ Dans le cas du type de dessin p31m, on peut prendre comme polygone minimal un triangle équilatéral dont tous les sommets sont des centres de tiers de tour du dessin. Soit I un sommet du triangle. En doublant ce triangle grâce à une symétrie par rapport à un des côtés d'extrémité I, on obtient un losange. En prenant ce losange et ses images par les deux rotations de centre I et d'angles +120° et -120°, on obtient pour polygone translaté adapté un hexagone régulier inscriptible. Les vecteurs des translations minimales sont portés par des "petites diagonales" de cet hexagone.

¤ Dans le cas du type de dessin p4g, on peut prendre comme polygone minimal un triangle rectangle isocèle dont le sommet principal, noté I, est le centre d'un quart de tour du dessin invariant, et les deux autres sommets les centres voisins de symétries centrales du dessin. En doublant ce triangle par symétrie par rappport à sa base, on obtient un carré. En prenant ce carré et ses images par les rotations de centre I et d'angles respectifs +90°, 180°, -90°, on obtient pour polygone translaté adapté un parallélogramme de base qui est aussi un carré.

Pour plus de beauté et de virtuosité dans la construction des dessins - comme dans ceux d'Escher ou de M. Raba (voir "Le monde des pavages" cité dans la bibliographie) - et pour la réalisation de pavages figuratifs à motifs simples, il faut comprendre mieux encore les propriétés du polygone minimal. Voir pour cela la fiche 3.5 et l'ouvrage cité.

Haut de page

sommaire  parcourir le dossier