C. Drouin
Bordeaux, novembre 2002
| 3.4. Réalisation de dessins symétriques glissés |
| Équipe académique mathématiques C. Drouin Bordeaux, novembre 2002 |
On ne considère ici que des dessins doublement périodiques ayant les deux propriétés suivantes :
¤ Ils sont invariants par des symétries centrales, ou par des symétries axiales, ou par des symétries glissées.
¤ Ils ne sont invariants par aucune rotation, sauf, éventuellement, des symétries centrales.
Au sommaire de cette page
|
A. Analyse des dessins symétriques et glissés |
 |
A. Analyse de dessins symétriques et
glissés ![]()
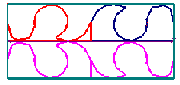
Analyser le dessin
Comme toujours, pour analyser un dessin doublement périodique, il faut mettre en évidence les vecteurs des translations de base, les axes de symétrie, les centres des rotations (ici des demi-tours), les réflexions glissées...
On peut également repérer les parallélogrammes de base, et mieux encore, les motifs minimaux, les polygones minimaux et les ensembles translatés adaptés construits à partir du polygone minimal ou du motif minimal.
Classification de ces dessins
On peut démontrer que l'on peut classifier les dessins ainsi déterminés en distinguant les cas suivants :
- Dessin de type pm (M1 kangourou). Le dessin admet des axes de symétrie tous parallèles, mais pas de centre de symétrie. Il n'admet pas de symétries glissées autres que celles composées de réflexions et de translations du dessin.
- Dessin de type p2 (R2 kangourou). Le dessin admet des centres de symétrie, mais pas de symétrie glissée ni de symétrie axiale.
- Dessin de type pg (M0g kangourou). Le dessin admet des symétries glissées, mais pas de symétrie axiale ni centrale.
- Dessin de type cm (M1g kangourou). Le dessin admet des axes de symétrie tous parallèles, mais pas de centre de symétrie. Il admet des symétries glissées autres que celles composées de réflexions et des translations du dessin.
- Dessin de type pmg (M1R2). Le dessin admet des axes de symétrie tous parallèles, ainsi que des centres de symétrie.
- Dessin de type pgg (M0R2). Le dessin n'admet pas de réflexion, mais admet des réflexions glissées et des symétries centrales.
- Dessin de type pmm (M2). Le dessin admet deux ensembles de réflexions, chacun correspondant à une direction des axes de symétrie, ces deux directions étant orthogonales entre elles. Les seuls centres de symétrie sont à l'intersection des axes de symétrie.
- Dessin de type cmm (M2R2). Le dessin admet deux ensembles de réflexions, chacun correspondant à une direction des axes de symétrie, ces deux directions étant orthogonales entre elles. Les intersections des axes sont bien sûr des centres de symétrie, mais il y a d'autres centres de symétrie, à mi-distance entre les axes.
Activités mathématiques
Pour telle ou telle catégorie de pavages rotatifs, observer et décrire la "trame" de ce pavage, c'est-à-dire les positions mutuelles des vecteurs des translations, des centres et des axes de symétrie, des axes et des vecteurs des glissages.
Déterminer graphiquement un parallélogramme de base du pavage et, mieux encore, un motif minimal, un polygone minimal et les ensembles translatés adaptés construits à partir du polygone minimal ou du motif minimal.
Éventuellement, démontrer que dans tel type de pavage, les positions mutuelles des vecteurs des translations, des centres de symétrie des rotations, des axes de symétrie, sont nécessairement celles qui sont constatées visuellement. On pourra pour cela composer les diverses isométries du pavage.
Par exemple, répondre mathématiquement aux questions suivantes :
- Pourquoi l'intersection de deux axes de symétrie est-elle toujours un centre de symétrie ?
- On se place dans le cas où le dessin admet deux réflexions d'axes parallèles, translatés l'un de l'autre par tw, le vecteur w étant normal aux axes. Pourquoi la translation t2w laisse-t-elle alors le dessin invariant ?
Pour répondre mathématiquement à ces questions, il faut déterminer la composée de deux réflexions d'axes perpendiculaires, ou d'axes parallèles.
B. Méthode de construction des dessins
symétriques glissés ![]()
On entreprend ici de construire des dessins symétriques ou glissés.
Pour pouvoir construire soi-même un dessin, il faut faire à l'envers la démarche d'analyse précédente. On va partir cette fois du polygone minimal, des isométries du dessin et du parallélogramme adapté de base, pour arriver à dessiner notre dessin de type donné.
Voici un exemple utilisant l'outil "polygone" de Cabri-géomètre (pour généraliser, voir le paragraphe suivant qui donne dans chaque cas le polygone minimal).
Il s'agit de construire un dessin, sur le thème des vagues, de type pmg (voir les caractéristique dans le paragraphe A).
Comme exposé dans le paragraphe C, le polygone minimal correspondant est (par exemple) un rectangle, dont deux côtés parallèles sont des axes de symétrie du dessin, et dont les milieux des autres côtés sont des centres de symétries du même dessin.
On suppose que les axes de symétrie sont portés par les côtés horizontaux du rectangle minimal et que les centres de symétrie sont les milieux des côtés verticaux. On choisit le motif minimal en faisant en sorte que le dessin passe par les centres de symétrie aux milieux des côtés verticaux.

Comme spécifié ci-dessus, on passe du motif minimal au rectangle minimal adapté en effectuant une symétrie par rapport à un centre de symétrie, puis une symétrie axiale par rapport à un côté horizontal :

On obtient l'ensemble du dessin en translatant le parallélogramme (rectangle) minimal par rapport à ses côtés :
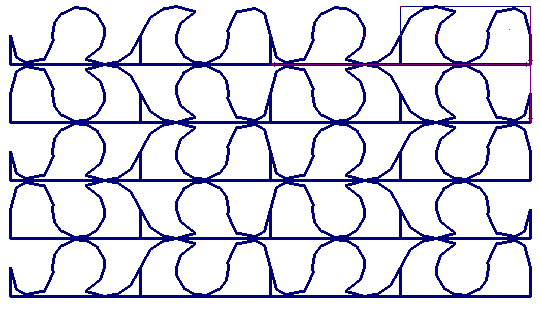
On voit ainsi apparaître le dessin avec des vagues, de type pmg. Celui-ci admet aussi un glissage, composé d'une réflexion et d'une symétrie centrale du dessin.
Du pur point de vue esthétique - et non plus mathématique -, on pourra décorer le dessin, le remplir, pour mieux faire apparaître l'idée initiale de vagues :
2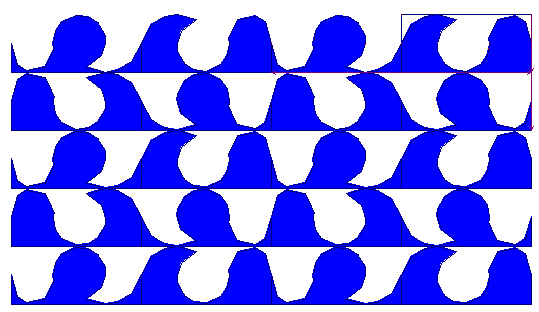 2
2
Attention cependant : ainsi rempli, si on s'oblige à tenir compte des couleurs, le dessin n'est plus de type pmg, mais seulement de type pg. Il n'y a plus aucune symétrie, que des glissages.
En toute rigueur, le dessin rempli de type pmg est le suivant :

...mais on perd l'idée de vague (on pourrait modifier ce dessin pour y faire apparaître divers types d'oiseaux...).
Pour plus de beauté et de virtuosité dans la construction des dessins - comme dans ceux d'Escher ou de M. Raba (voir "Le monde des pavages" cité dans la bibliographie) - et pour la réalisation de pavages figuratifs à motifs simples, il faut comprendre mieux encore les propriétés du polygone minimal. Voir pour cela la fiche 3.5 et l'ouvrage cité.
Le paragraphe C qui suit donne les polygones minimaux et les polygones translatés adaptés pour toutes les classes de dessins étudiées dans cette fiche.
C. Polygones minimaux des dessins symétriques
et glissés ![]()
Soit pour analyser, soit surtout pour construire un dessin de type donné parmi ceux étudiés ici, on a besoin de la forme d'un polygone minimal et de celle du parallélogramme de base adapté correspondant ou, lorsque ce dernier n'existe pas, du polygone translaté adapté correspondant.
- Dans le cas du type de dessin pm, on peut prendre comme polygone minimal un rectangle dont un des côtés est axe de symétrie du dessin. En doublant le rectangle par symétrie relativement à cet axe, on obtient un parallélogramme de base adapté qui est un rectangle.
- Dans le cas du type de dessin p2, on peut prendre comme polygone minimal un parallélogramme dont les sommets ainsi que les milieux de deux côtés opposés sont des centres de symétrie du dessin, voisins entre eux. En doublant le parallélogramme par symétrie par rapport à l'un de ces points, on obtient un parallélogramme de base adapté.
- Dans le cas du type de dessin pg, on peut prendre comme polygone minimal un rectangle dont un côté porte un vecteur d'une translation minimale du dessin, tandis que les deux côtés qui lui sont orthogonaux portent des axes de glissage du dessin, ainsi que la moitié d'un autre vecteur de translation minimale du dessin. En doublant ce rectangle par glissage ayant pour axe l'un des ses côtés, on obtient un parallélogramme de base adapté, qui est lui aussi un rectangle.
- Dans le cas du type de dessin cm, on peut prendre comme polygone minimal un rectangle dont deux côtés opposés portent des axes de symétrie consécutifs du dessin, ainsi que le vecteur d'un glissage minimal, et dont les diagonales portent les vecteurs des translations minimales du dessin. En doublant ce rectangle par symétrie par rapport à un de ses côtés, on obtient un polygone translaté adapté qui est un rectangle. Dans ce cas, il n'existe pas de parallélogramme de base qui soit adapté. Remarquons au passage que les parallélogrammes de base sont des losanges.
- Dans le cas du type de dessin pmg, on peut prendre comme polygone minimal un rectangle dont deux côtés opposés portent deux axes de symétrie parallèles consécutifs du dessin, et dont les autres côtés ont pour milieu des centres de symétries du dessin. En faisant une symétrie centrale par rapport à un de ces points, puis une réflexion par rapport à un de ces côtés, on obtient un parallélogramme de base, adapté, qui est ici un rectangle.
- Dans le cas du type de dessin pgg, on peut prendre comme polygone minimal un rectangle dont les quatre sommets sont des centres de symétrie du dessin, voisins entre eux, et admettant comme axe de symétrie un axe de symétrie d'un glissage du dessin. En doublant le rectangle à l'aide de ce glissage, puis en doublant de nouveau grâce à une symétrie centrale, on obtient un parallélogramme de base, adapté, qui est un rectangle.
- Dans le cas du type de dessin pmm, on peut prendre comme polygone minimal un rectangle dont les quatre côtés portent des axes de symétrie du dessin, voisins entre eux. Par deux symétries axiales successives ayant pour axes deux côtés perpendiculaires du rectangle minimal, on obtient à partir de ce rectangle un parallélogramme de base, adapté.
- Dans le cas du type de dessin cmm, on peut prendre comme polygone minimal un rectangle dont trois côtés portent des axes de symétrie du dessin, voisins entre eux, et dont le quatrième a pour milieu un centre de symétrie. En faisant une symétrie centrale par rapport à ce point, puis successivement deux réflexions par rapport aux côtés du rectangle minimal, on obtient un parallélogramme de base, qui est ici un rectangle, d'aire huit fois plus grande que le rectangle minimal.
Pour plus de beauté et de virtuosité dans la construction des dessins - comme dans ceux d'Escher ou de M. Raba (voir "Le monde des pavages" cité dans la bibliographie) - et pour la réalisation de pavages figuratifs à motifs simples, il faut comprendre mieux encore les propriétés du polygone minimal. Voir pour cela la fiche 3.5 et l'ouvrage cité.
![]() sommaire
sommaire ![]() parcourir le dossier
parcourir le dossier ![]()