C. Drouin
Bordeaux, novembre 2002
| 3.5. Réalisation de dessins bipériodiques figuratifs |
| Équipe académique mathématiques C. Drouin Bordeaux, novembre 2002 |
Au sommaire de cette page
A. Principe
B. Exemple
C. Recollement et pliages du polygone minimal
Cette fiche présente la réalisation de pavages plus esthétiques, dits figuratifs.
Dans ce cas, l'ensemble minimal est construit avec une forme figurative (un objet, un animal, un personnage...). Autrement dit, les contours de l'ensemble minimal font partie du motif.
Le décor apparaît alors comme la répétition d'une seule forme.
Il est souvent utile dans ce cas de colorer les différents exemplaires du dessin avec plusieurs couleurs, pour que le décor soit plus lisible. Le dessin apparaît alors manifestement comme un pavage, le pavé naturel étant évidemment le motif minimal figuratif.
La construction de tels motifs minimaux ayant une forme reconnaissable n'est pas facile et requiert des connaissances particulières.
La première étape est, comme indiqué sur les fiches précédentes, de choisir un type de pavage et de connaître le polygone minimal correspondant.
Mais cette fois, il faut jouer sur plusieurs polygones minimaux, et non plus seulement sur un seul, comme précédemment.
Lorsqu'on dessine le motif minimal dans le polygone minimal, il est parfois bon de sortir du polygone minimal pour poursuivre le dessin de façon esthétique. Le dessin déborde alors dans un polygone voisin. Attention, ce polygone est une copie du minimal ; ou encore le polygone minimal est une copie du polygone voisin, par une isométrie f.
Il faut donc copier dans le polygone minimal la partie du motif tracée dans le polygone voisin, par l'intermédiaire de l'isométrie f.
Il est possible de faire ceci en décalquant ou en découpant et recollant. C'est ce que les logiciels de pavages (Ornament, Kali,...) font de façon automatique. Mais il est plus instructif de le réaliser soi-même.
On veut, par exemple, réaliser un pavage artistique de type p3 dont le motif minimal est un poisson. La fiche 3.3 précise que dans ce cas le polygone minimal est un losange IJKL formé de deux triangles équilatéraux. Les sommets du losange sont les centres de tiers de tour laissant le pavage invariant.
Les figures qui suivent ont été réalisées avec le logiciel Cabri-géomètre, qui est tout-à-fait efficace pour ce genre de constructions, tout en laissant à l'utilisateur le plaisir de les décider lui-même. On se sert de façon essentielle de l'outil "polygone" de Cabri.
On décide de construire la tête du poissson (un polygone) sur un des côtés du losange minimal. Elle dépasse donc du losange.
Il faut donc la faire tourner autour du point K. (angle de +120°). La partie inférieure va être enlevée au losange. Elle se copie en quelque sorte en négatif.
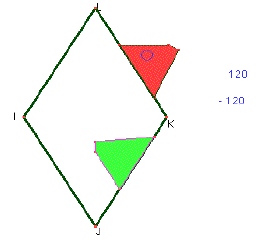
De la même façon, si on construit une arête dorsale à partir du point L (en rouge), on doit appliquer à cette forme la rotation de centre I et d'angle -120°, et la forme image (en vert) doit être découpée du losange.
Inversement, si on découpe un morceau du dos du poissson, au dessus de I, ce morceau, tourné de -120° autour de I, se rajoute au bas du losange.
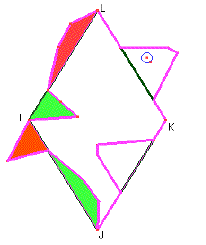
La figure suivante montre le motif minimal achevé : on peut le décorer et le colorier. On voit aussi sur cette figure le polygone translaté (un hexagone).
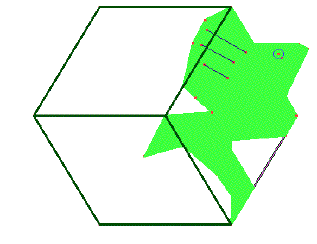
Grâce aux tiers de tours autour de I, on passe du motif minimal à l'ensemble translaté adapté formé de trois poissons.
Enfin, par des translations ou par des rotations du motif minimal, on peut réaliser le pavage complet.
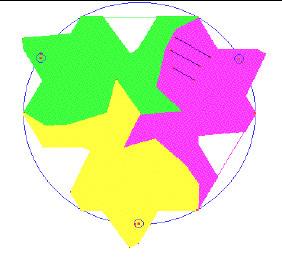


La dernière figure est réalisée en juxtaposant plusieurs des images précédentes à l'aide d'un logiciel standard de traitement d'images (par copier/coller)
C. Recollements et pliages du polygone minimal
![]()
Losrque on franchit la frontière du polygone minimal, on se retrouve dans un polygone voisin. Mais ce polygone voisin va lui-même se retrouver copié, par une isométrie, dans le polygone minimal dont on est parti, comme ci-dessus.

Il se passe ce phénomène surprenant que, sorti du polygone minimal par une frontière on y rentre par une autre frontière, parfois fort éloignée. Dans l'exemple considéré, cela se traduit ainsi : la flèche du dessus en violet, se poursuit en la flèche inférieure de la même couleur ; la flèche du dessus en vert, se poursuit en la flèche inférieure de la même couleur.
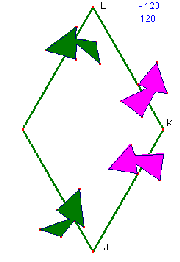
Quand on considère ce pavage, on doit admettre que dans le polynôme minimal, les frontières [KL] et [KJ] sont confondues, le collage s'effectuant, sur la figure ci-dessous, dans le sens indiqué par les triangles. De même pour les frontières [IL] et [IJ].
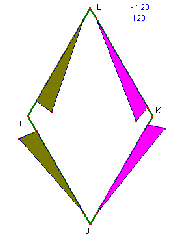
D'un point de vue mathématique, ces identifications conduisent aux concepts fort raffinés de topologie et géométrie quotients, hors de propos ici. Il s'agit d'espaces qui ne sont pas simplement des parties du plan.
D'un point de vue plus concret, ces identifications permettent, de simplifier le confection du motif minimal, en collant provisoirement les frontières ainsi identifiées, grâce à un pliage du losange autour de [IK]. On réalise le motif sur le polygone plié, puis on le déplie pour réaliser le pavage : c'est la technique de l'enveloppe de M. Raba. Voir "le Monde des Pavages", qui propose un certain nombre de ces techniques de pliage-collage.
Si l'on désire une présentation théorique et des applications pratiques de ces espaces, on pourra aussi consulter l'adresse Internet suivante :
http://comp.uark.edu/~cgstraus/symmetry.unit/index.html (en anglais).
On consultera en particulier les sections 2 et 3, les espaces concernés ici étant nommés "Orbitfolds".
De toute façon, pour réaliser ce type de pavages figuratifs, il est nécessaire de comprendre, ne serait-ce qu'intuitivement, ces recollements du polygone minimal sous l'effet des isométries du pavage.
![]() sommaire
sommaire ![]() parcourir le dossier
parcourir le dossier ![]()