Mathématiques et maîtrise de la langue |
|
Animations ZAP 2005 et 2006 |
|
Dans le cadre du plan académique de formation, huit ZAP ont bénéficié, en 2005, d'une journée de réflexion sur le thème Mathématiques et maîtrise de la langue. Cette action a été reconduite en 2006 et le sera en 2007.
Le calendrier
En 2005 les réunions ont eu lieu
![]() Le 12 janvier, pour les ZAP de Blaye et Oloron
Le 12 janvier, pour les ZAP de Blaye et Oloron
![]() Le 26 janvier, pour les ZAP de Bergerac et Bayonne-Anglet-Biarritz
Le 26 janvier, pour les ZAP de Bergerac et Bayonne-Anglet-Biarritz
![]() Le 9 février, ZAP Bordeaux-Rive droite et Marmande
Le 9 février, ZAP Bordeaux-Rive droite et Marmande
![]() Le 16 février, ZAP de Libourne et Dax
Le 16 février, ZAP de Libourne et Dax
En 2006 les réunions ont eu (ou auront) lieu
![]() Le 26 avril, pour la ZAP Médoc
Le 26 avril, pour la ZAP Médoc
![]() Le 3 mai, pour les ZAP de Dordogne Est – Périgueux et Mérignac
– Pessac
Le 3 mai, pour les ZAP de Dordogne Est – Périgueux et Mérignac
– Pessac
![]() Le 17 mai, pour les ZAP d’Arcachon et Mont de Marsan
Le 17 mai, pour les ZAP d’Arcachon et Mont de Marsan
![]() Le 31 mai, pour la ZAP Villeneuve – Fumel
Le 31 mai, pour la ZAP Villeneuve – Fumel
![]() Le 7 juin, pour la ZAP Langon et Orthez
Le 7 juin, pour la ZAP Langon et Orthez

Les objectifs
La maîtrise de la langue joue un rôle central dans tous les enseignements mais revêt des aspects particuliers en mathématiques. L'élève doit acquérir un vocabulaire spécifique et ayant parfois un sens différent de celui qu'il a dans le langage usuel. Il est aussi confronté aux difficultés de lecture et d'écriture liées aux caractéristiques des textes mathématiques qui sont très concis avec une grande part d'implicite.
L'objectif du stage est donc d'amener les collègues à prendre conscience que le professeur de mathématiques a son rôle à jouer pour aider les élèves autour de la problématique de la maîtrise de la langue.
Ce stage essaie de donner des pistes pour aider les élèves à mieux lire un texte mathématique et à mieux écrire des mathématiques. Comment rendre l'élève moins passif devant un texte écrit, et permettre aux mathématiques de ne pas apparaître comme un monde à part ?
Le choix a été fait de ne pas parler de la rédaction des démonstrations qui était traitée lors d'autres stages.
Le déroulement
La première partie du stage consiste à essayer d'établir une typologie des textes mathématiques comme il en existe une en français. Pour cela, les stagiaires travaillent sur des extraits de textes mathématiques en essayant de les regrouper en catégories, en choisissant des critères de tri qui leur paraissent les plus appropriés.
La synthèse met en évidence la complexité de la syntaxe et la multiplicité des textes mathématiques auxquels sont confrontés les élèves, très tôt et simultanément, d'où la nécessité d'être très clair avec les élèves sur les textes que l'on propose. Quand on choisit un texte, il faudrait évaluer ce qui peut rendre, a priori, difficile la compréhension de l'élève (vocabulaire - place de la question - difficultés syntaxiques). On peut poser des questions pour aider l'élève à trier les informations et l'amener à les utiliser dans un certain ordre.
On s'intéresse ensuite à quelques pages de manuels scolaires pour identifier ces différents types de textes, regarder s'ils sont clairement repérés et également analyser le rôle joué par les illustrations. Cela permet de faire apparaître la nécessité d'aider les élèves dans la lecture autonome de leur manuel.
Dans une seconde partie, toujours en liaison avec la lecture, on s'interroge sur les erreurs que peuvent commettre les élèves en faisant une mauvaise lecture de l’énoncé ou de la consigne. On propose ensuite des exercices de formes différentes pour faire prendre conscience aux élèves de l’importance de la lecture du texte. L’étude de quelques manuels de sixième montre les réels progrès faits en ce sens par les auteurs.
Deux exemples de travail spécifique en devoir à la maison permettent de repérer des difficultés supplémentaires (extraits de mathadoc, Issa et Moussa) :
Issa : http://www.mathadoc.com/Documents/college/6eme/6operdec/autre2.PDF
Moussa : http://www.mathadoc.com/Documents/college/6eme/6operdec/autre3.PDF
Corrigé avec un diaporama pdf (6 Mo) proposé par une collègue de l’académie.
Comment rendre les élèves plus acteurs ?
Un collègue de l’académie a réalisé un travail sous forme d'exercices interactifs proposé en téléchargement pour un usage en salle informatique avec les élèves de sixième.
Voir le travail Télécharger le travail (pages html compressées, 121 Ko)
Afin de cerner plus précisément les problèmes de lecture d'énoncé, il a semblé intéressant de faire travailler les élèves sur des énoncés invraisemblables, à savoir des exercices infaisables par manque d'informations ou des exercices mathématiquement faisables mais n'ayant aucun sens pratique ("dans un minibus, il y a 350 personnes..."). La fiche proposée comporte une série de tels exercices auxquels ont été ajoutés des énoncés réalistes et faisables.
Après discussion, il apparaît évident qu'un tel document n'est pas à utiliser dans son intégralité avec des élèves mais peut faire l'objet d'un travail plus morcelé.
Dans un travail de groupe, l'autocorrection peut amener un élève à corriger un camarade pour s'apercevoir ensuite qu'il a fait la même erreur.
La troisième partie du stage consiste à présenter deux expériences d'écriture de textes mathématiques par les élèves.
![]() Écriture d'un programme de construction en 6e
Écriture d'un programme de construction en 6e
Les enseignants présents au stage ont exprimé leurs doutes quant à l'efficacité des figures téléphonées pour convaincre les élèves de la nécessité de respecter certains critères, puisqu'ils arrivent toujours à se faire comprendre, à leur manière. On propose alors une activité qui tente d'y remédier, en faisant retravailler les élèves sur leurs propres productions – par exemple à partir d'un exercice des cahiers d'évaluation 6e – dans le but de les améliorer et de dégager une liste de critères à respecter. Les élèves s'approprient ainsi réellement les critères retenus et réalisent une affiche qui reste sur le mur de la classe et à laquelle on fera référence à chaque écriture de programme de construction. Elle pourra également être modifiée, complétée si besoin est tout au long de l'année.
 |
 |
![]() Narration de recherche
Narration de recherche
Nous nous plaignons souvent que les élèves n'écrivent pas quand on leur donne un problème à chercher ; l'idée est de leur proposer un problème ouvert pouvant être résolu de différentes façons avec une consigne particulière : « Vous raconterez sur votre feuille les différentes étapes de votre recherche (vous pouvez minuter le temps, joindre vos brouillons...), les observations que vous avez pu faire et qui vous ont fait progresser ou changer de méthode (il vaut mieux chercher seul mais...). L'évaluation ne portera pas sur la nature de la solution (juste, fausse, incomplète...) mais sur les trois points évoqués ci-dessus. »
L'examen de quelques copies d'élèves sur différents sujets permet d'illustrer ce qu'ils peuvent écrire dans un tel contexte, d'amorcer une discussion sur les points forts, notamment en termes de motivation et d'investissement de l'élève dans la recherche, mais aussi les limites d'une telle pratique, liées notamment au choix du sujet et à l'évaluation. On peut envisager l’évaluation de ce type de travail en rendant les copies avec une grille d’évaluation sous forme de tableau :
Si "oui" . cocher 1a case correspondante |
oui |
L'élève a expérimenté |
|
L'élève a émis une conjecture acceptable (qui peut être fausse.. ) |
|
L'élève s'est engagé dans une démarche ou une stratégie pertinente (même si elle n'a pas abouti) |
|
L'élève a donné des indications sur la stratégie qu'il a choisie |
|
L'élève a respecté les notations et s'est montré précis au niveau du vocabulaire mathématique |
|
L'élève a employé un français correct et s'est exprimé avec clarté |
|
L'élève a fait preuve d'esprit critique |
|
Présence d' incohérence(s) ou de résultat(s) aberrant(s) |
|
Présence de "faute(s) de logique" |
|
Présence d'une démonstration (correcte ou non) : calculs. enchaînement de propriétés élémentaires |
ou encore une grille en étoile, listant des critères différents de ceux ciblés dans les devoirs plus classiques : |
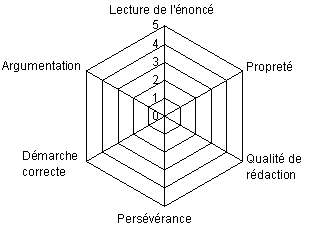 |
Exemple de sujet et d'une copie d'élève de 5e.
Des actions possibles au niveau de l'établissement
![]() Suite aux évaluations en 6e, une rencontre entre enseignants
du primaire et du collège permet d'élaborer un document de liaison
école primaire-collège, dans le but d'éviter une trop grande
rupture.
Suite aux évaluations en 6e, une rencontre entre enseignants
du primaire et du collège permet d'élaborer un document de liaison
école primaire-collège, dans le but d'éviter une trop grande
rupture.
![]() Dans un collège, l'équipe pédagogique se met d'accord sur
le vocabulaire, les définitions et les notations utilisées de
la 6eà la 3e ; l'établissement participe
aussi à des réunions inter-cycle 3e-2e.
Dans un collège, l'équipe pédagogique se met d'accord sur
le vocabulaire, les définitions et les notations utilisées de
la 6eà la 3e ; l'établissement participe
aussi à des réunions inter-cycle 3e-2e.
![]() Les programmes laissant une certaine latitude dans la façon d'aborder
les contenus, on peut au niveau de l'équipe pédagogique réfléchir
à la façon d'anticiper certaines difficultés et rendre
l'apprentissage plus progressif.
Les programmes laissant une certaine latitude dans la façon d'aborder
les contenus, on peut au niveau de l'équipe pédagogique réfléchir
à la façon d'anticiper certaines difficultés et rendre
l'apprentissage plus progressif.
![]() Des réunions interdisciplinaires mathématiques-français
sont l'occasion d'échanger sur les difficultés communes.
Des réunions interdisciplinaires mathématiques-français
sont l'occasion d'échanger sur les difficultés communes.
Un exemple d'IDD en classe de 5e, où les élèves ont à créer un dictionnaire de Mathématiques sur le modèle d'un dictionnaire de Français
Quelques pistes de réflexion
![]() Les objectifs des programmes visent à développer des compétences
générales, comme l'esprit critique, l'argumentation...
Les objectifs des programmes visent à développer des compétences
générales, comme l'esprit critique, l'argumentation...
Toutes les disciplines contribuent à la formation du citoyen.
Les mathématiques constituent une entrée importante pour maîtriser la langue ; plus le milieu social est défavorisé, plus l'entrée par la littérature est difficile et l'entrée par les sciences peut être intéressante.
« Il est en effet possible de se livrer, à partir d'un nombre limité de connaissances, à une activité mathématique véritable, avec son lot de questions ouvertes, de recherches pleines de surprises, de conclusions dont on parvient à se convaincre. Une telle activité, accessible aux élèves, a une valeur formatrice évidente et leur permet d'acquérir les savoirs et savoir-faire qui leur seront nécessaires. » (extrait de l'introduction générale des programmes 2005 pour le collège)
![]() Au primaire, l'élève travaille sur le mode narratif. Ce qu'il
lit ou ce qu'il produit possède un dénouement clairement identifié
à la fin du document. En classe de sixième, nos textes mathématiques
ne présentent pas cette structure linéaire et demandent une lecture
réfléchie plus morcelée. L'emploi des connecteurs logiques -
parce que, car , donc – est une source de difficultés.
Au primaire, l'élève travaille sur le mode narratif. Ce qu'il
lit ou ce qu'il produit possède un dénouement clairement identifié
à la fin du document. En classe de sixième, nos textes mathématiques
ne présentent pas cette structure linéaire et demandent une lecture
réfléchie plus morcelée. L'emploi des connecteurs logiques -
parce que, car , donc – est une source de difficultés.
En mathématiques, le discours argumentatif est déductif. En français, le discours argumentatif cherche à convaincre en faisant une liste d'arguments qui n'est pas forcément une chaîne déductive, et l'argumentation peut être démontée. De plus, l'argumentation n'est abordée dans cette discipline qu'en fin de classe de quatrième.
Bibliographie
Liens web
Travail effectué en classe de 6e, dans le cadre des heures d'Aide au Travail Personnel
De nombreux exemples de narration de recherche, IREM de Montpellier
Ecrire, penser, parler en mathématiques, Académie de Créteil
Mathématiques et maîtrise de la langue, Repères IREM n°39