Mathématiciens de la page d'accueil

mathématiciens

Gauss, comme Cauchy, se trouve à la charnière entre l'époque classique des mathématiques, inaugurée par Newton et Leibniz, dominée par Euler, et ce que l'on pourrait appeler l'époque moderne, qui commence avec, par exemple, Cantor. A la fois, il obtient des résultats remarquables à l'intérieur de théories déjà anciennes, mais aussi il découvre de nouveaux objets, nouvelles méthodes, comme a dit Jean Dieudonné (Pour l'honneur de l'esprit humain, Hachette, Chapitre V). Gauss a laissé des découvertes dans un nombre impressionnant de domaines des mathématiques. Enfant prodige, calculateur fantastique, esprit extrêmement créatif et profond, son génie était reconnu de son vivant, et il avait gagné le sunom mérité de Prince des mathématiciens.

A l'âge de dix-neuf ans, il démontre ce résultat nouveau et remarquable que le polygone régulier à 17 côtés est constructible à la règle et au compas. (Ce théorème est lié à la résolution dans C de l'équation z^17-1 = 0, et relève de l'algèbre et de la théorie des nombres.) Bien plus jeune, à l'école primaire, il avait étonné son maître en calculant en un temps record la somme des 100 premiers entiers, que le maître avait donné à faire à ses élèves pour avoir la paix. (La méthode qu'il avait utilisée est classique, mais est fort astucieuse de la part d'un enfant de moins de dix ans).

Dans le domaine de la l'Arithmétique (ou Théorie des Nombres), il publie en 1801 ses Disquisitiones Arithmeticae. Il définit les congruences modulo n (deux nombres sont congruents modulo n si n divise leur différence). Il s'intéresse particulièrement au problèmes des résidus quadratiques : Quels sont les entiers qui, modulo n, sont congrus à un carré ? Il fait aussi faire de gros progrès à l'étude des formes quadratiques binaires, c'est-à-dire à la recherche des entiers annulant l'expression ax^2+bxy+cy^2-k. A propos de ses recherches en arithmétique, Gauss est amené à se placer dans C, et à considérer les complexes de la forme a+ib, a et b étant réels, appelés désormais entiers de Gauss. (Voir par exemple Chapitre V, par W. et F. Ellison, de l'Abrégé d'Histoire des mathématiques, par Jean Dieudonné, chez Herman).

Dans le domaine de l'Analyse, Gauss s'intéresse comme d'ailleurs Cauchy, aux fonctions de C dans lui même. Il démontre par exemple que tout polynôme admet au moins une solutions dans C (Théorème fondamental de l'algèbre). Il retrouve beaucoup des résultats de Cauchy en ce domaine, mais ne les publie pas, pas plus qu'un grand nombre des théorèmes originaux qu'il découvre. Il est un ardent propagandiste de la vision géométrique des nombres complexes, telle qu'elle est présentée de nos jours aux élèves de Terminales.

Son oeuvre est importante également en Géométrie Différentielle. Il définit par exemple la courbure de Gauss en un point d'une surface, et étudie les géodésiques de ces surfaces. (Voir par exemple Chapitre IX, par Paulette Libermann Ellison, de l'ouvrage cité plus haut de Jean Dieudonné).

Gauss s'est intéressé également à l'atronomie, à la géodésie, au magnétisme, toutes sciences qu'il a fait progresser...Il a inventé la Méthode des moindres carrés. On lui doit aussi la fameuse loi de Laplace-Gauss pour une variable aléatoire, loi de densité f(x)=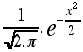, qui fait partie du prochain programme de Terminale S.

Les parents de Gauss étaient de simples ouvriers. Devenu célèbre, il continue de mener une vie fort discrète. Vers la fin de sa vie, il forme divers étudiants, dont Eisenstein, Riemann, Dedekind...