Formation et évaluation des élèves en S et ES |
|
Équipe académique Mathématiques |
|
Dans le cadre du plan académique de formation, sept regroupements sur le thème Formation et évaluation des élèves dans les séries S et ES ont été organisés à l'attention de tous les lycées par les IA-IPR de mathématiques, courant novembre et décembre 2004.
Ces journées ont permis de présenter de nombreuses informations, de réfléchir et d'échanger à propos de l'évolution des modalités du baccalauréat en séries S et ES (QCM, questions ouvertes, restitution de connaissance) et des épreuves orales du second groupe.
Plusieurs professeurs de chaque établissement (de un à quatre) étaient invités à représenter leurs collègues à ces réunions.
Au sommaire de cette page
Fonctions, suites, QCM, ROC
10 novembre |
au lycée Jay de Baufort PERIGUEUX et |
24 novembre |
au lycée Sud-Médoc TAILLAN-MEDOC et |
8 décembre |
au lycée Alfred Kastler TALENCE et |
15 décembre |
au lycée Saint-Cricq PAU |
Matin
![]() Intervention
de l'IA-IPR animateur de la journée
Intervention
de l'IA-IPR animateur de la journée
![]() Deux
ateliers en parallèle :
Deux
ateliers en parallèle :
"Les QCM" et "L'oral en mathématiques au second groupe d'épreuves du bac"
Après midi
![]() Deux
ateliers en parallèle
Deux
ateliers en parallèle
"Les questions ouvertes" et "La restitution organisée de connaissances"
![]() Synthèse
des travaux en ateliers, échange final
Synthèse
des travaux en ateliers, échange final
(IA-IPR animateur de la journée)
Pourquoi fait-on évoluer les épreuves de baccalauréat ?
La quasi-totalité des élèves issus des séries S et ES continue les études en sections de techniciens supérieurs, en université ou en classes préparatoires ; ces études demandent une capacité à mobiliser rapidement de nombreux savoirs ou savoir-faire et à prendre des initiatives. Il est donc important de développer ces compétences dès le secondaire.
Or la formation en lycée a connu une dérive importante : elle a été de plus en plus centrée sur la préparation du baccalauréat au détriment d'une formation adaptée aux études supérieures et ce, pour essentiellement deux raisons.
D'une part le public en lycée a évolué, et pour les enseignants, l'année est souvent une course contre le temps.
D'autre part, les sujets proposés étaient devenus stéréotypés et risquaient d'engendrer en amont une formation des élèves trop limitée, pouvant parfois relever du conditionnement. De plus, les textes de devoirs à la maison durant l'année étaient souvent extraits des annales (cela ne veut pas dire qu'il ne faut pas en faire, mais il est essentiel de ne pas limiter les recherches à cela). Des élèves ayant une vision incertaine des mathématiques s'engageaient dans des études scientifiques et découvraient trop tardivement que cette discipline est tout autre. De leur côté, les collègues des filières d'enseignement supérieur ne pouvaient que déplorer les savoirs limités des étudiants et leur incapacité à réagir devant une situation nouvelle.
Une évolution était donc nécessaire.
Elle s'appuie sur deux leviers :
![]() de nouveaux
programmes sont entrés en vigueur en terminale à la rentrée 2002 ;
ils insistent en particulier sur les quatre composantes de l'activité mathématique :
observation, abstraction, réflexion, démonstration, ainsi que sur la nécessité
de faire fonctionner les contenus en situation et de choisir des activités faisant
intervenir plusieurs connaissances en même temps ;
de nouveaux
programmes sont entrés en vigueur en terminale à la rentrée 2002 ;
ils insistent en particulier sur les quatre composantes de l'activité mathématique :
observation, abstraction, réflexion, démonstration, ainsi que sur la nécessité
de faire fonctionner les contenus en situation et de choisir des activités faisant
intervenir plusieurs connaissances en même temps ;
![]() les sujets
de baccalauréat sont appelés à évoluer consécutivement à ce
changement de programmes de façon à
les sujets
de baccalauréat sont appelés à évoluer consécutivement à ce
changement de programmes de façon à
![]() mieux
couvrir le programme par le nombre et la diversité des exercices ;
mieux
couvrir le programme par le nombre et la diversité des exercices ;
![]() rendre
l'épreuve moins stéréotypée ;
rendre
l'épreuve moins stéréotypée ;
![]() tester
l'aptitude des élèves à prendre des initiatives et à mobiliser
rapidement plusieurs outils ;
tester
l'aptitude des élèves à prendre des initiatives et à mobiliser
rapidement plusieurs outils ;
![]() s'intégrer
dans une formation scientifique générale ;
s'intégrer
dans une formation scientifique générale ;
![]() éviter
le bachotage et proposer une épreuve plus attractive prenant mieux en compte les
aptitudes des élèves.
éviter
le bachotage et proposer une épreuve plus attractive prenant mieux en compte les
aptitudes des élèves.
C'est ainsi que l'épreuve a été renouvelée et modulée de façon à permettre la formation souhaitée pour les études supérieures, tout en garantissant la progressivité de ces changements.
Les textes (BO n° 19 du 8mai 2003) précisent :
« l'épreuve est destinée à évaluer la façon dont les candidats ont atteint les grands objectifs de formation mathématique visés par le programme de la série S :
![]() acquérir
des connaissances et les organiser ;
acquérir
des connaissances et les organiser ;
![]() mobiliser des notions, des résultats et des méthodes utiles dans le cadre
de la résolution d'exercices ;
mobiliser des notions, des résultats et des méthodes utiles dans le cadre
de la résolution d'exercices ;
![]() prendre des initiatives ;
prendre des initiatives ;
![]() comprendre et construire un raisonnement ;
comprendre et construire un raisonnement ;
![]() mettre en forme un raisonnement mathématique, une démonstration. »
mettre en forme un raisonnement mathématique, une démonstration. »
ou de la série ES :
![]() acquérir des connaissances et les organiser ;
acquérir des connaissances et les organiser ;
![]() maîtriser la lecture et le traitement de l'information (graphique, algébrique,
numérique)
maîtriser la lecture et le traitement de l'information (graphique, algébrique,
numérique)
![]() savoir lier dans une même démarche observation, imagination, questionnement,
synthèse, logique, argumentation et démonstration mathématique »
savoir lier dans une même démarche observation, imagination, questionnement,
synthèse, logique, argumentation et démonstration mathématique »
La session 2004 a présenté les premières innovations : quatre exercices en série ES, dont l'un proposant un QCM ; cinq exercices en série S, l'un avec un QCM et un autre avec une question "un peu" ouverte.
Pour la session 2005, la maquette s'applique intégralement : restitution organisée de connaissances (une démonstration pouvant être demandée en série S), question ouverte envisageable en fin d'exercice (on parle de question ouverte, demandant la mise en ouvre d'outils simples, pas de problème ouvert ; il ne s'agit pas de demander une recherche lourde).
La banque d'exercices a été enrichie courant décembre 2004 par des exercices comportant une restitution organisée de connaissances et, pour la série S, des démonstrations de cours.
Les exercices classiques sont toujours d'actualité ; des exercices novateurs sont proposés dans les banques, mais il a bien été précisé que les exercices figurant dans les annales constituent naturellement des exemples pour la confection des sujets.
Voir texte Inspection Générale.
Il n'est pas réaliste d'envisager de former les élèves en vue de cette évolution la seule année de terminale. Cette formation doit s'étaler sur tout le lycée et même en collège.
Au lycée, le travail doit ainsi être préparé dès la classe de seconde ; dans ce cadre, il faut envisager en seconde des devoirs à la maison dont on diversifie les contenus, en proposant par exemple des exercices facultatifs. Cette préparation sera intensifiée en 1re S, sans perdre de vue qu'il faut laisser le temps aux élèves de s'adapter.
Au cours de certaines journées, un questionnaire d'enquête sur les modalités d'évaluation et les pratiques d'enseignement, établi par l'inspection générale, a été proposé aux collègues, qui l'ont renseigné.
Il pourra être également proposé lors d'entretiens avec des équipes pédagogiques ou lors de regroupements.
L'inspecteur animateur a pu proposer les réflexions suivantes
À propos des fonctions
![]() On
voit souvent des études de fonctions "en aveugle" et le même plan
d'étude de fonction que dans les années 1950. Ce n'est plus pertinent. Des
outils permettent de visualiser la courbe d'une fonction, et le premier travail est de s'en
servir.
On
voit souvent des études de fonctions "en aveugle" et le même plan
d'étude de fonction que dans les années 1950. Ce n'est plus pertinent. Des
outils permettent de visualiser la courbe d'une fonction, et le premier travail est de s'en
servir.
![]() Il
ne s'agit ni d'examiner la parité d'une liste de fonctions, ni de bannir toute question
touchant cette propriété ; ce qu'il faut, c'est apprendre aux élèves à discerner
s'il est nécessaire ou non d'étudier la parité d'une fonction.
Il
ne s'agit ni d'examiner la parité d'une liste de fonctions, ni de bannir toute question
touchant cette propriété ; ce qu'il faut, c'est apprendre aux élèves à discerner
s'il est nécessaire ou non d'étudier la parité d'une fonction.
![]() Il
est plus cohérent d'étudier le sens de variation d'une fonction avant de rechercher
les limites (du global au plus particulier).
Il
est plus cohérent d'étudier le sens de variation d'une fonction avant de rechercher
les limites (du global au plus particulier).
![]() Enfin,
une étude de fonction doit servir à quelque chose ; étudier une
fonction pour tracer sa courbe et ne rien en faire ensuite n'est pas motivant.
Enfin,
une étude de fonction doit servir à quelque chose ; étudier une
fonction pour tracer sa courbe et ne rien en faire ensuite n'est pas motivant.
À propos des suites
L'exercice 15 page 16 de la banque mise en ligne en décembre 2003 propose l'étude d'une suite homographique selon deux méthodes. La première est graphique, la deuxième repose sur l'utilisation d'une suite auxiliaire.
Dans bien des manuels, on ne trouve que la deuxième méthode : c'est un travail technique sans beaucoup d'intérêt. Il faut revoir les pratiques afin de donner du sens aux activités.
À propos des QCM
Fabriquer des QCM intelligents n'est pas évident ! Si pour traiter le QCM il faut faire l'exercice, le QCM est inutile, posons plutôt l'exercice lui-même.
On souhaite rendre l'élève critique, l'entraîner à voir la plausibilité des résultats. Le QCM doit permettre de mettre en ouvre une autre forme de travail intellectuel que les exercices classiques.
À propos des questions « ROC »
Les questions « ROC » peuvent inclure, en série S, une démonstration de cours ; il ne s'agit pas de favoriser le bachotage sur les démonstrations que le programme demande explicitement de faire (bien que connaître dix ou douze démonstrations ne soit pas mauvais pour un élève de TS !).
Ce qui est important, c'est de faire des démonstrations en classe en mettant clairement en valeur les démarches et surtout en expliquant comment l'élève pourrait découvrir seul de telles stratégies.
Par exemple lorsqu'il s'agit de démontrer que toute fonction f solution
de l'équation différentielle y' = a y est de la forme  , donner la fonction
, donner la fonction 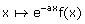 et prouver que cette fonction est constante n'est que
de très faible intérêt. En revanche, faire reconstituer la démarche
qui amène à considérer
et prouver que cette fonction est constante n'est que
de très faible intérêt. En revanche, faire reconstituer la démarche
qui amène à considérer 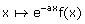 est réellement très formateur.
est réellement très formateur.
Il est vrai que cela prend du temps. Comment en libérer ?
Dans beaucoup de cas, les cours contiennent trop de formules ; il faudrait au contraire stimuler l'aptitude à connaître les formules essentielles et à en retrouver d'autres.
Attention aussi aux corrections d'exercices très longues ; il s'agit de faire ressortir les idées-clés sans faire tout le détail des calculs.
Plusieurs collègues évoquent les énormes difficultés rencontrées en calcul par les élèves, ainsi que les abus d'utilisation de la calculatrice ou le stockage de résultats dans les calculatrices.
Il faut apprendre aux élèves à se servir de la calculatrice, ce qui ne veut pas dire qu'il faut l'utiliser sans arrêt. On a le droit de l'interdire à certains moments. En ce qui concerne le stockage des résultats, il faudrait arriver à leur faire comprendre que l'on a besoin de connaître les résultats (par exemple quelques formules trigonométriques) si on veut être capable de les reconnaître.
![]() Les
exercices comportant une Reconnaissance Organisée de Connaissances (ROC)
Les
exercices comportant une Reconnaissance Organisée de Connaissances (ROC)
![]() L'oral
du second groupe d'épreuves du baccalauréat
L'oral
du second groupe d'épreuves du baccalauréat
![]() Les
exercices comportant une Reconnaissance Organisée de Connaissances (ROC)
Les
exercices comportant une Reconnaissance Organisée de Connaissances (ROC)
![]() L'oral
du second groupe d'épreuves du baccalauréat
L'oral
du second groupe d'épreuves du baccalauréat